Leonardi.DB - Diagrams

General

Date

Treat uncertainty ranges strict

Contributors

Exactly these contributors

Information

Has a legend
Yes No

Has a caption
Yes No

Contains errors
Yes No

Tags

Exactly these tags

Logic

Aristotelian family

Proper interpretation (see hierarchy)

Boolean complexity

Treat uncertainty ranges strict

Vertex labels

Include diagrams with a single label
Include diagrams with multiple labels

Uniqueness

Vertices are unique up to logical equivalence
Yes No

Geometry

Geometric shape

Proper interpretation (see hierarchy)

Regular
Yes No

Geometric representation of contradiction

By central symmetry

By diametric opposition (but no central symmetry)

By some other geometric feature

N.A.

Geometric complexity

Has non-zero colinearity, coplanarity or cospatiality
Yes No

Style: general

Visuals

Colored
Yes No

Embellished
Yes No

Information

Contains conceptual info
Yes No

Contains mnemonic info
Yes No

Contains definitions
Yes No

Style: vertex labels

Label type

Exactly these label types

Linguistic characteristics

Language

Exactly these languages

Lexical field

Exactly these fields

Contains abbreviations
Yes No

Contains partial sentences
Yes No

Symbolic characteristics

Symbolic field

Exactly these fields

Logical system

Exactly these systems

Mathematical branch

Exactly these branches

Contains partial formulas
Yes No

Bitstring characteristics

Contains protobitstrings
Yes No

Style: edge labels

Label type

Exactly these label types

Linguistic characteristics

Language

Exactly these languages

Contains abbreviations
Yes No

Contains single words
Yes No

Symbolic characteristics

Symbolic field

Exactly these fields

Logical system

Exactly these systems

Mathematical branch

Exactly these branches

Contains partial formulas
Yes No

Bitstring characteristics

Contains protobitstrings
Yes No

Style: diagram form

Vertex form

Exactly these forms

Edge form

Exactly these forms

Contains arrowheads
Yes No

Contains overlapping edges
Yes No

Contains curved edges
Yes No

Contains hooked edges
Yes No

Contains vertex-wide edges
Yes No

Contains text in edges
Yes No

Source	Date (min⁠–⁠max)	Aristotelian Family	B.C. (min⁠–⁠max)	Geometric Shape
The Genesis of the Truth-Table Device, p. 60, by Anellis, Irving H.	2004	Contrariety 4-clique	4	Tetrahedron
Frege's Lectures on Logic. Carnap's Student Notes 1910-1914, p. 69, by Frege, Gottlob; Carnap, Rudolf; Reck, Erich H. (ed.); Awodey, Steve (ed.)	2004	Classical Logical Graph	3	Digon
Nearly Every Normal Modal Logic is Paranormal, p. 280, by Marcos, João	2005	Classical Sigma-2	3	Square
Nearly Every Normal Modal Logic is Paranormal, p. 291, by Marcos, João	2005	Classical Sigma-2	3	Square
Towards a Mental Probability Logic, p. 94, by Pfeifer, Niki; Kleiter, Gernot D.	2005	Non-Sigma	9	Rectangle
A Pragmatic Logic of Scientific Discovery, p. 232, by Sallantin, Jean; Dartnell, Christopher; Afshar, Mohammad	2006	Classical Sigma-2	3	Rectangle
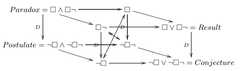A Pragmatic Logic of Scientific Discovery, p. 234, by Sallantin, Jean; Dartnell, Christopher; Afshar, Mohammad	2006	Jacoby-Sesmat-Blanché Sigma-3	3	Rectangular Cuboid
A Pragmatic Logic of Scientific Discovery, p. 234, by Sallantin, Jean; Dartnell, Christopher; Afshar, Mohammad	2006	Jacoby-Sesmat-Blanché Sigma-3	3	Rectangular Cuboid
A Generalization of Hume's Thesis, p. 111, by Woleński, Jan	2006	Classical Sigma-2	3	Square
A Generalization of Hume's Thesis, p. 112, by Woleński, Jan	2006	Sigma-4 Graph	4–16	Square
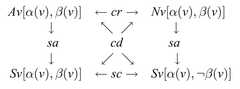Relevant Restricted Quantification, p. 590, by Beall, JC; Brady, Ross T.; Hazen, Allen P.; Priest, Graham; Restall, Greg	2006	Classical Sigma-2	3	Rectangle
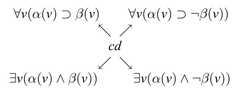Relevant Restricted Quantification, p. 590, by Beall, JC; Brady, Ross T.; Hazen, Allen P.; Priest, Graham; Restall, Greg	2006	Degenerate Sigma-2 with Unconnectedness 4	4	Rectangle
Deontic Logic, p. 201, by McNamara, Paul	2006	Classical Sigma-2	3	Square
Deontic Logic, p. 203, by McNamara, Paul	2006	Classical Sigma-2	3	Square
Deontic Logic, p. 203, by McNamara, Paul	2006	Non-Sigma	3	Hexagon
Deontic Logic, p. 210, by McNamara, Paul	2006	Classical Sigma-2	3	Square
Deontic Logic, p. 248, by McNamara, Paul	2006	Classical Sigma-2	3	Square
A.N. Prior's Logic, p. 408, by Øhrstrøm, Peter; Hasle, Per	2006	Classical Sigma-2	3	Rectangle
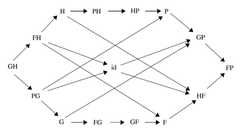A.N. Prior's Logic, p. 429, by Øhrstrøm, Peter; Hasle, Per	2006	Non-Sigma		Hexagon
Deontic Logic, p. 274, by McNamara, Paul	2006	Non-Sigma		Octadecagon
Deontic Logic, p. 275, by McNamara, Paul	2006	Non-Sigma		Octadecagon
Quantifiers in Language and Logic, p. 23, by Peters, Stanley; Westerståhl, Dag	2006	Classical Sigma-2	3	Square
Quantifiers in Language and Logic, p. 25, by Peters, Stanley; Westerståhl, Dag	2006	Degenerate Sigma-2 with Unconnectedness 4	4	Square
Fuzzy Quantifiers. A Computational Theory, p. 95, by Glöckner, Ingo	2006	Classical Sigma-2	3	Square
Fuzzy Quantifiers. A Computational Theory, p. 120, by Glöckner, Ingo	2006	Sigma-2 Graph	3–4	Square