A Pragmatic Logic of Scientific Discovery (2006), p. 234
by Sallantin, Jean; Dartnell, Christopher; Afshar, Mohammad

Copyright according to our policy

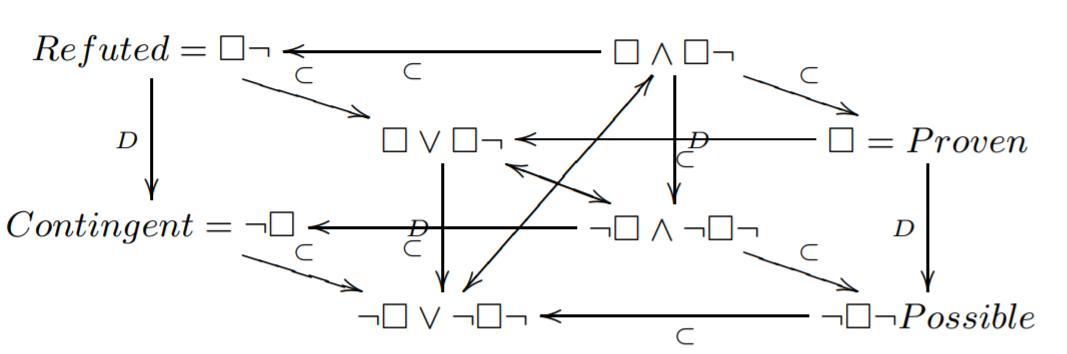
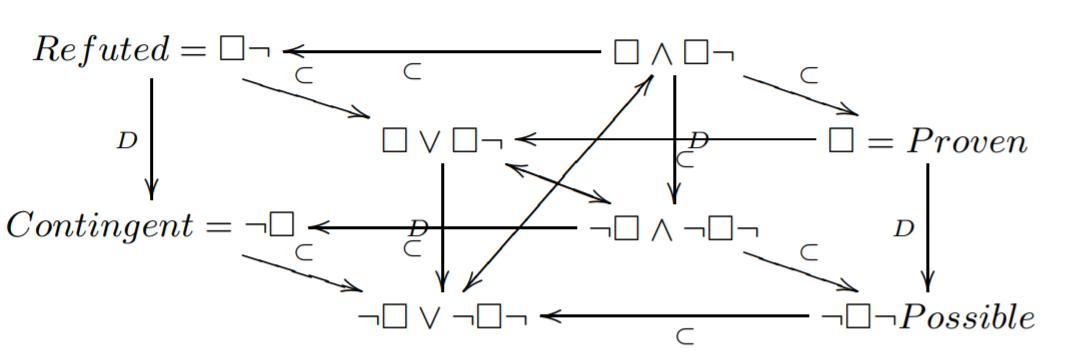
Caption

Square of oppositions resulting from C1 logic, as a diagonal plane of the Cube

Logic

Aristotelian family

Jacoby-Sesmat-Blanché Sigma-3

Boolean complexity

3

Number of labels per vertex (at most)

2

Equivalence between (some) labels of the same vertex

No

Analogy between (some) labels of the same vertex

No

Uniqueness of the vertices up to logical equivalence

Yes

Errors in the diagram

No

Geometry

Shape

Rectangular Cuboid (irregular)

Colinearity range

0

Coplanarity range

0

Cospatiality range

0

Representation of contradiction

By central symmetry

Vertex description

Conceptual info

No

Mnemonic support (AEIO, purpurea ...)

No

Form

none

Label type

linguistic

,

symbolic

Language

English

Contains partial sentences or single words

Yes

Contains abbreviations

No

Symbolic field

logic

Contains partial formulas or symbols

Yes

Logical system

modal logic

Edge description

Style

Diagram is colored

No

Diagram is embellished

No

Tags

Boolean closed

;

non-contingent formulas

Additional notes

This diagram assumes the modal logic KD in the background (otherwise, the subalternations marked with 'D' would not hold). But working in KD also means that $\Box \wedge \Box\neg$ is a contradiction and that $\neg\Box \vee \neg\Box\neg$ is a tautology. In other words, this diagram explicitly contains two non-contingent formulas (apart from those two, it is a JSB sigma-3).