You're using an ancient browser to surf the modern web. Please update to the latest version (and don't use Internet Explorer!).

Leonardi.DB
a logical geometry project

Diagrams (1 to 25 of 5649)

Searching for diagrams matching all criteria ...

Diagram Source Date
(min⁠–⁠max)
Aristotelian Family
 		B.C.
(min⁠–⁠max)
Geometric Shape
http://purl.org/lg/diagrams/beziau_2012_the-new-rising-of-the-square-of_1dvf8i5fn_p-13_1ee7qv4tp The New Rising of the Square of Opposition, p. 13, by Beziau, Jean-Yves 2012 Sigma-6 Graph 4 Two Dimensional Shape
http://purl.org/lg/diagrams/gildin_1970_aristotle-and-the-moral-square-of_1dnandt4a_p-102_1eedpvbff Aristotle and the Moral Square of Opposition, p. 102, by Gildin, Hilail 1970 Non-Sigma 3 Two Dimensional Shape
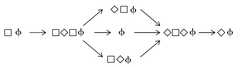http://purl.org/lg/diagrams/gregory_2015_language-and-logics-an-introduction_1i45i188t_p-108_1i5knponq Language and Logics. An Introduction to the Logical Foundations of Language, p. 108, by Gregory, Howard 2015 Non-Sigma Two Dimensional Shape
http://purl.org/lg/diagrams/luzeaux-et-al-_2008_logical-extensions-of_1dv12vgm7_p-179_1ecktdkkh Logical Extensions of Aristotle's Square, p. 179, by Luzeaux, Dominique; Sallantin, Jean; Dartnell, Christopher 2008 Jacoby-Sesmat-Blanché Sigma-3 4 Triangular Prism
http://purl.org/lg/diagrams/luzeaux-et-al-_2008_logical-extensions-of_1dv12vgm7_p-179_1ecktisvp Logical Extensions of Aristotle's Square, p. 179, by Luzeaux, Dominique; Sallantin, Jean; Dartnell, Christopher 2008 Jacoby-Sesmat-Blanché Sigma-3 4 Triangular Prism
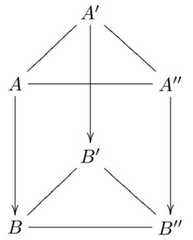http://purl.org/lg/diagrams/angot-pellissier_2008_-setting-n-opposition_1dr1l86qf_p-240_1ede03uuk "Setting" n-Opposition, p. 240, by Pellissier, Régis 2008 Non-Sigma 4 Triangular Prism
http://purl.org/lg/diagrams/dekker_2017_logical-conversions_1dnchu634_p-196_1f5j4nb9u Logical Conversions, p. 196, by Dekker, Paul 2017 Jacoby-Sesmat-Blanché Sigma-3 4 Triangular Prism
http://purl.org/lg/diagrams/dekker_2017_logical-conversions_1dnchu634_p-199_1f5j55dkv Logical Conversions, p. 199, by Dekker, Paul 2017 Jacoby-Sesmat-Blanché Sigma-3 4 Triangular Prism
http://purl.org/lg/diagrams/dekker_2017_logical-conversions_1dnchu634_p-199_1f5j5932c Logical Conversions, p. 199, by Dekker, Paul 2017 Jacoby-Sesmat-Blanché Sigma-3 4 Triangular Prism
http://purl.org/lg/diagrams/dekker_2017_logical-conversions_1dnchu634_p-199_1f5j5bo6e Logical Conversions, p. 199, by Dekker, Paul 2017 Jacoby-Sesmat-Blanché Sigma-3 4 Triangular Prism
http://purl.org/lg/diagrams/dekker_2015_not-only-barbara_1e00iucgr_p-122_1f60dlcau Not Only Barbara, p. 122, by Dekker, Paul 2015 Jacoby-Sesmat-Blanché Sigma-3 4 Triangular Prism
http://purl.org/lg/diagrams/dekker_2015_not-only-barbara_1e00iucgr_p-123_1f60ducl6 Not Only Barbara, p. 123, by Dekker, Paul 2015 Degenerate Sigma-3 with Unconnectedness 4 5 Triangular Prism
http://purl.org/lg/diagrams/cavaliere_2017_iconic-and-dynamic-models-to_1dvi3a0f7_p-274_1g7f3rmpe Iconic and Dynamic Models to Represent "Distinctive" Predicates: The Octagonal Prism and the Complex Tetrahedron of Opposition, p. 274, by Cavaliere, Ferdinando 2017 Jacoby-Sesmat-Blanché Sigma-3 3 Triangular Prism
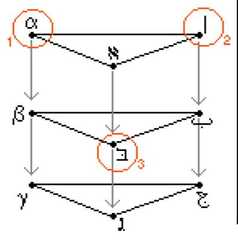http://purl.org/lg/diagrams/moretti_2009_the-geometry-of-logical-opposition_1dnbb3upn_p-192_1i4jqt0r8 The Geometry of Logical Opposition, p. 192, by Moretti, Alessio 2009 Triangular Prism
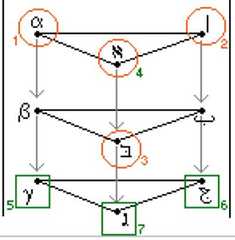http://purl.org/lg/diagrams/moretti_2009_the-geometry-of-logical-opposition_1dnbb3upn_p-192_1i4jqvspl The Geometry of Logical Opposition, p. 192, by Moretti, Alessio 2009 Triangular Prism
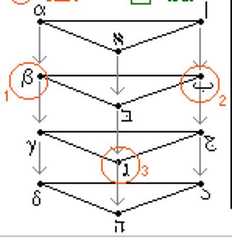http://purl.org/lg/diagrams/moretti_2009_the-geometry-of-logical-opposition_1dnbb3upn_p-192_1i4jr2a2h The Geometry of Logical Opposition, p. 192, by Moretti, Alessio 2009 Triangular Prism
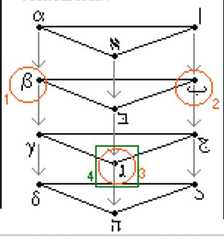http://purl.org/lg/diagrams/moretti_2009_the-geometry-of-logical-opposition_1dnbb3upn_p-192_1i4jr7vvm The Geometry of Logical Opposition, p. 192, by Moretti, Alessio 2009 Triangular Prism
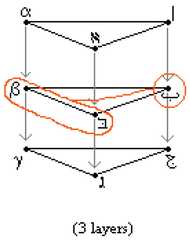http://purl.org/lg/diagrams/moretti_2009_the-geometry-of-logical-opposition_1dnbb3upn_p-286_1i5aepcbn The Geometry of Logical Opposition, p. 286, by Moretti, Alessio 2009 Triangular Prism
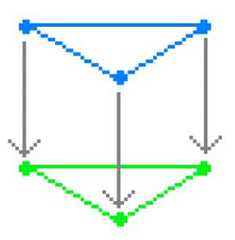http://purl.org/lg/diagrams/moretti_2009_the-geometry-of-logical-opposition_1dnbb3upn_p-296_1i5ajjv25 The Geometry of Logical Opposition, p. 296, by Moretti, Alessio 2009 Triangular Prism
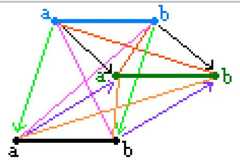http://purl.org/lg/diagrams/moretti_2009_the-geometry-of-logical-opposition_1dnbb3upn_p-344_1i69b8dle The Geometry of Logical Opposition, p. 344, by Moretti, Alessio 2009 Triangular Prism
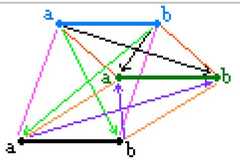http://purl.org/lg/diagrams/moretti_2009_the-geometry-of-logical-opposition_1dnbb3upn_p-344_1i69bea81 The Geometry of Logical Opposition, p. 344, by Moretti, Alessio 2009 Triangular Prism
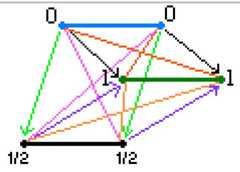http://purl.org/lg/diagrams/moretti_2009_the-geometry-of-logical-opposition_1dnbb3upn_p-347_1i69g8c05 The Geometry of Logical Opposition, p. 347, by Moretti, Alessio 2009 Triangular Prism
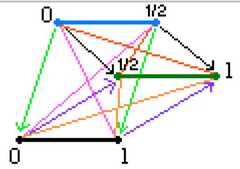http://purl.org/lg/diagrams/moretti_2009_the-geometry-of-logical-opposition_1dnbb3upn_p-347_1i69gce8g The Geometry of Logical Opposition, p. 347, by Moretti, Alessio 2009 Triangular Prism
http://purl.org/lg/diagrams/moretti_2009_the-geometry-of-logical-opposition_1dnbb3upn_p-347_1i69gl3a3 The Geometry of Logical Opposition, p. 347, by Moretti, Alessio 2009 Triangular Prism
http://purl.org/lg/diagrams/moretti_2009_the-geometry-of-logical-opposition_1dnbb3upn_p-347_1i69go9hq The Geometry of Logical Opposition, p. 347, by Moretti, Alessio 2009 Triangular Prism
↑ Back to top ↑