Logical Extensions of Aristotle's Square (2008), p. 179
by Luzeaux, Dominique; Sallantin, Jean; Dartnell, Christopher

Copyright according to our policy

Logic

Aristotelian family

Jacoby-Sesmat-Blanché Sigma-3

Boolean complexity

4

Number of labels per vertex (at most)

1

Uniqueness of the vertices up to logical equivalence

No

Errors in the diagram

No

Geometry

Shape

Triangular Prism

Colinearity range

0–1

Coplanarity range

0

Cospatiality range

0

Representation of contradiction

By some other geometric feature

Vertex description

Conceptual info

No

Mnemonic support (AEIO, purpurea ...)

No

Form

none

Label type

generic placeholders

Edge description

Style

Diagram is colored

No

Diagram is embellished

No

Additional notes

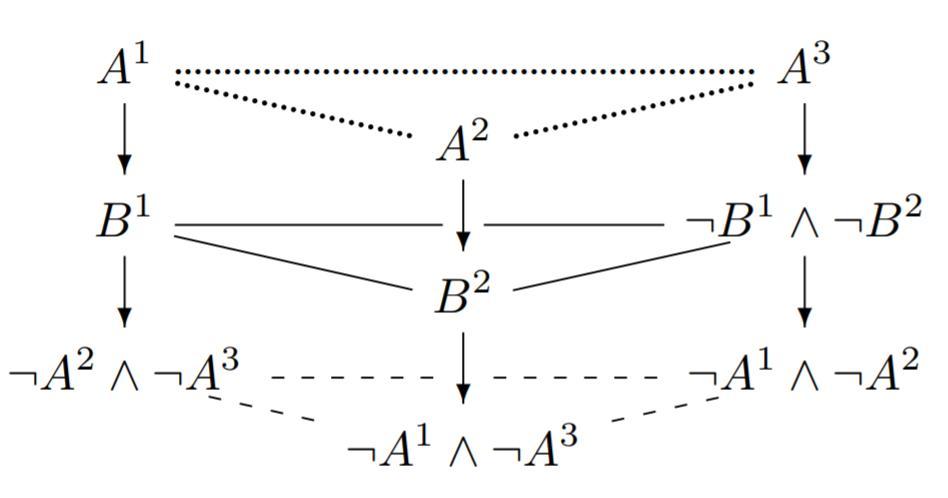
Each $B^i$ is equivalent to either $A^i$ above it or $C^i$ below it. Two of the $B$'s are equivalent to their corresponding $A$'s above, while the remaining third $B$ is equivalent to its corresponding $C$ below. After all, if $B^i \equiv A^i$ and $B^j \equiv A^j$, then $B^k \equiv \neg B^i \wedge \neg B^j \equiv \neg A^i \wedge \neg A^j \equiv C^k$.