Not Only Barbara (2015), p. 123
by Dekker, Paul
Copyright according to our policy
- Aristotelian family
- Degenerate Sigma-3 with Unconnectedness 4
- Boolean complexity
- 5
- Number of labels per vertex (at most)
- 1
- Uniqueness of the vertices up to logical equivalence
- Yes
- Errors in the diagram
- No
- Shape
- Triangular Prism (irregular)
- Colinearity range
- 0
- Coplanarity range
- 0
- Cospatiality range
- 0
- Representation of contradiction
- By some other geometric feature
Logic
Geometry
- Conceptual info
- No
- Mnemonic support (AEIO, purpurea ...)
- No
- Form
- none
- Label type
- linguistic
- Language
- English
- Lexical field
- temporal
- Contains partial sentences or single words
- Yes
- Contains abbreviations
- No
- Contains definitions of relations
- No
- Form
- solid lines ,
- none
- Has arrowheads
- No
- Overlap
- No
- Curved
- No
- Hooked
- No
- As wide as vertices
- No
- Contains text
- No
- Label type
- none
Vertex description
Edge description
- Diagram is colored
- No
- Diagram is embellished
- No
Style
Additional notes
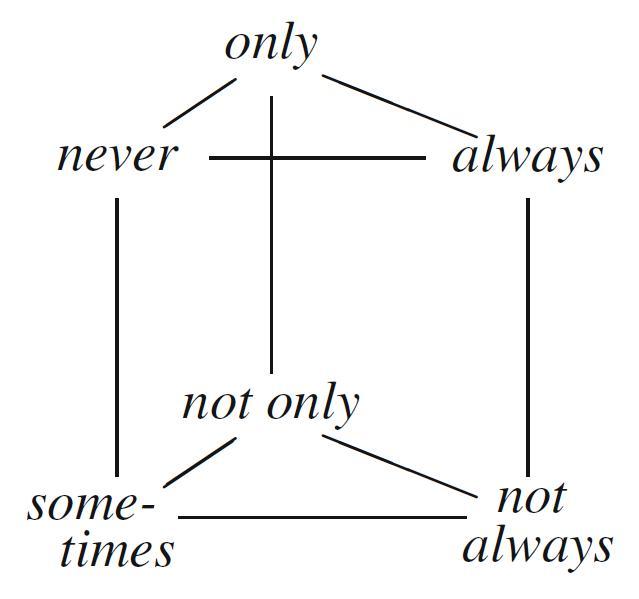
- This diagram is a U4 sigma-3 (rather than a JSB sigma-3), because here the assumption of 'differential import' (cf. p. 100) does not make sense anymore. For example, consider 'always' and 'only'. In a JSB sigma-3, these two items should be contrary to each other, whereas in a U4 sigma-3 they should be unconnected/independent. And as a matter of fact, it is clear that they are unconnected, in particular, the following two sentences (cf. p. 123) can be true together:
Don always talks nonsense when he is drunk.
Don only talks nonsense when he is drunk.
These two sentences are true together in a situation where Don talks nonsense exactly whenever he is drunk. This implies a violation of the 'differential import' assumption, but it constitutes perfectly imaginable situation.
The partition induces by this U4 sigma-3 (subject to existential, but not differential import) consists of the following five anchor formulas (cf. the Gergonne relations!):
$\bullet$ always $\wedge$ only
$\bullet$ always $\wedge$ not only
$\bullet$ sometimes $\wedge$ not always $\wedge$ not only
$\bullet$ not always $\wedge$ only
$\bullet$ never