|  | The Klein Group, Squares of Opposition and the Explanation of Fallacies in Reasoning, p. 386, by Robert, Serge; Brisson, Janie | 2016 | A Single PCD | 2 | Digon |
| 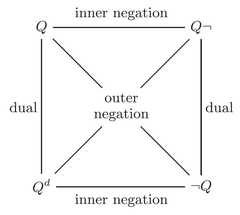 | Generalized quantifiers, p. 218, by Westerståhl, Dag | 2016 | Sigma-2 Graph | 3–4 | Square |
|  | Negation, p. 469, by de Swart, Henriëtte | 2016 | Classical Sigma-2 | 3 | Square |
|  | The Neo-Molinist Square Collapses: A Molinist Response to Elijah Hess, p. 198, by MacGregor, Kirk R. | 2016 | Classical Sigma-2 | 3 | Rectangle |
| 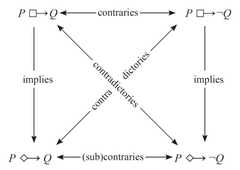 | The Neo-Molinist Square Collapses: A Molinist Response to Elijah Hess, p. 206, by MacGregor, Kirk R. | 2016 | Classical Sigma-2 | 3 | Rectangle |
|  | On Different Ways to be (dis)similar to Elements in a Set. Boolean Analysis and Graded Extension, p. 614, by Prade, Henri; Richard, Gilles | 2016 | Jacoby-Sesmat-Blanché Sigma-3 | 3 | Hexagon |
| 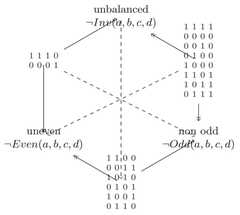 | On Different Ways to be (dis)similar to Elements in a Set. Boolean Analysis and Graded Extension, p. 614, by Prade, Henri; Richard, Gilles | 2016 | Jacoby-Sesmat-Blanché Sigma-3 | 3 | Hexagon |
| 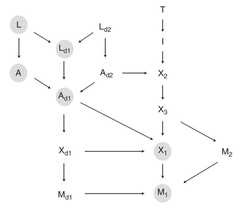 | The Logic of Modality, p. 354, by Strobino, Riccardo; Thom, Paul | 2016 | Non-Sigma | | Heptagon |
| 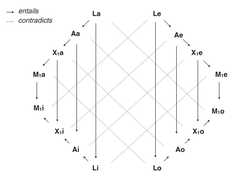 | The Logic of Modality, p. 356, by Strobino, Riccardo; Thom, Paul | 2016 | Sigma-8 Graph | | Octagon |
|  | Duality in Logic and Language, -, by Demey, Lorenz; Smessaert, Hans | 2016 | Classical Sigma-2 | 3 | Rectangle |
|  | Duality in Logic and Language, -, by Demey, Lorenz; Smessaert, Hans | 2016 | Classical Sigma-2 | 3 | Rectangle |
|  | Duality in Logic and Language, -, by Demey, Lorenz; Smessaert, Hans | 2016 | Classical Sigma-2 | 3 | Rectangle |
|  | Duality in Logic and Language, -, by Demey, Lorenz; Smessaert, Hans | 2016 | Jacoby-Sesmat-Blanché Sigma-3 | 3 | Hexagon |
|  | Duality in Logic and Language, -, by Demey, Lorenz; Smessaert, Hans | 2016 | Jacoby-Sesmat-Blanché Sigma-3 | 3 | Hexagon |
|  | Duality in Logic and Language, -, by Demey, Lorenz; Smessaert, Hans | 2016 | Classical Sigma-2 | 3 | Rectangle |
|  | Duality in Logic and Language, -, by Demey, Lorenz; Smessaert, Hans | 2016 | A Single PCD | 2 | Digon |
| 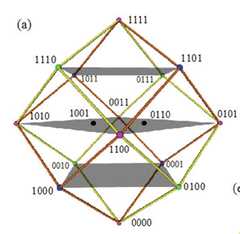 | Visualising the Boolean Algebra $\mathbb{B}_4$ in 3D, p. 291, by Smessaert, Hans; Demey, Lorenz | 2016 | Classical Sigma-7 | 4 | Rhombic Dodecahedron |
| 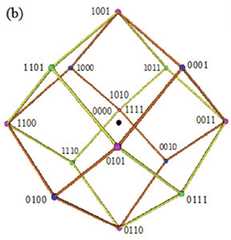 | Visualising the Boolean Algebra $\mathbb{B}_4$ in 3D, p. 291, by Smessaert, Hans; Demey, Lorenz | 2016 | Classical Sigma-7 | 4 | Rhombic Dodecahedron |
| 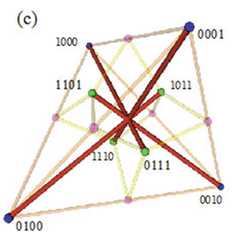 | Visualising the Boolean Algebra $\mathbb{B}_4$ in 3D, p. 291, by Smessaert, Hans; Demey, Lorenz | 2016 | Moretti-Pellissier Sigma-4 | 4 | Tetrahedron |
| 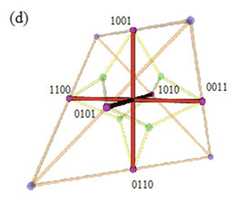 | Visualising the Boolean Algebra $\mathbb{B}_4$ in 3D, p. 291, by Smessaert, Hans; Demey, Lorenz | 2016 | Degenerate Sigma-3 with Unconnectedness 12 | 4 | Octahedron |
| 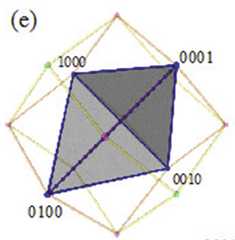 | Visualising the Boolean Algebra $\mathbb{B}_4$ in 3D, p. 291, by Smessaert, Hans; Demey, Lorenz | 2016 | Contrariety 4-clique | 4 | Tetrahedron |
| 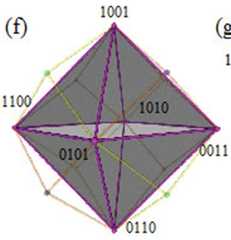 | Visualising the Boolean Algebra $\mathbb{B}_4$ in 3D, p. 291, by Smessaert, Hans; Demey, Lorenz | 2016 | Degenerate Sigma-3 with Unconnectedness 12 | 4 | Octahedron |
| 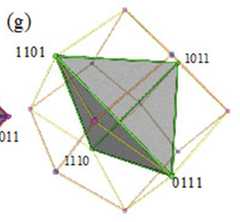 | Visualising the Boolean Algebra $\mathbb{B}_4$ in 3D, p. 291, by Smessaert, Hans; Demey, Lorenz | 2016 | Subcontrariety 4-clique | 4 | Tetrahedron |
| 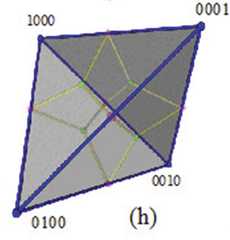 | Visualising the Boolean Algebra $\mathbb{B}_4$ in 3D, p. 291, by Smessaert, Hans; Demey, Lorenz | 2016 | Contrariety 4-clique | 4 | Tetrahedron |
| 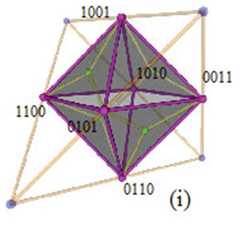 | Visualising the Boolean Algebra $\mathbb{B}_4$ in 3D, p. 291, by Smessaert, Hans; Demey, Lorenz | 2016 | Degenerate Sigma-3 with Unconnectedness 12 | 4 | Octahedron |