|  | An analogical hexagon, p. 9, by Beziau, Jean-Yves | 2018 | A Single PCD | 2 | Digon |
|  | An analogical hexagon, p. 9, by Beziau, Jean-Yves | 2018 | Contrariety 3-clique | 3 | Triangle |
|  | An analogical hexagon, p. 9, by Beziau, Jean-Yves | 2018 | A Single PCD | 2 | Digon |
|  | An analogical hexagon, p. 9, by Beziau, Jean-Yves | 2018 | Contrariety 3-clique | 3 | Triangle |
|  | An analogical hexagon, p. 9, by Beziau, Jean-Yves | 2018 | Jacoby-Sesmat-Blanché Sigma-3 | 3 | Hexagon |
| 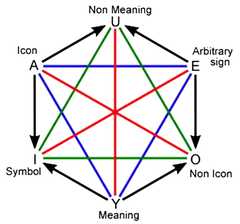 | An analogical hexagon, p. 10, by Beziau, Jean-Yves | 2018 | Jacoby-Sesmat-Blanché Sigma-3 | 3 | Hexagon |
|  | An analogical hexagon, p. 11, by Beziau, Jean-Yves | 2018 | Classical Sigma-2 | 3 | Rectangle |
|  | An analogical hexagon, p. 12, by Beziau, Jean-Yves | 2018 | Jacoby-Sesmat-Blanché Sigma-3 | 4 | Hexagon |
|  | An analogical hexagon, p. 12, by Beziau, Jean-Yves | 2018 | Contrariety 3-clique | 3–4 | Triangle |
|  | An analogical hexagon, p. 13, by Beziau, Jean-Yves | 2018 | Contrariety 4-clique | 4 | Tetrahedron |
|  | An analogical hexagon, p. 10, by Beziau, Jean-Yves | 2018 | Non-Sigma | 3 | Triangle |
|  | An analogical hexagon, p. 11, by Beziau, Jean-Yves | 2018 | Non-Sigma | 3 | Triangle |
|  | An analogical hexagon, p. 12, by Beziau, Jean-Yves | 2018 | Non-Sigma | 3 | Triangle |
|  | Computing the maximal Boolean complexity of families of Aristotelian diagrams, p. 1325, by Demey, Lorenz | 2018 | Classical Sigma-2 | 3 | Rectangle |
| 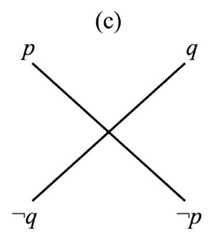 | Computing the maximal Boolean complexity of families of Aristotelian diagrams, p. 1325, by Demey, Lorenz | 2018 | Degenerate Sigma-2 with Unconnectedness 4 | 4 | Rectangle |
|  | Computing the maximal Boolean complexity of families of Aristotelian diagrams, p. 1325, by Demey, Lorenz | 2018 | Jacoby-Sesmat-Blanché Sigma-3 | 3 | Hexagon |
|  | Computing the maximal Boolean complexity of families of Aristotelian diagrams, p. 1325, by Demey, Lorenz | 2018 | Jacoby-Sesmat-Blanché Sigma-3 | 4 | Hexagon |
|  | Computing the maximal Boolean complexity of families of Aristotelian diagrams, p. 1325, by Demey, Lorenz | 2018 | Classical Sigma-2 | 3 | Rectangle |
|  | Computing the maximal Boolean complexity of families of Aristotelian diagrams, p. 1330, by Demey, Lorenz | 2018 | Classical Sigma-2 | 3 | Rectangle |
|  | Computing the maximal Boolean complexity of families of Aristotelian diagrams, p. 1330, by Demey, Lorenz | 2018 | Degenerate Sigma-2 with Unconnectedness 4 | 4 | Rectangle |
|  | Computing the maximal Boolean complexity of families of Aristotelian diagrams, p. 1330, by Demey, Lorenz | 2018 | Jacoby-Sesmat-Blanché Sigma-3 | 3–4 | Hexagon |
| 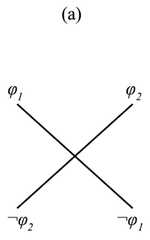 | Computing the maximal Boolean complexity of families of Aristotelian diagrams, p. 1334, by Demey, Lorenz | 2018 | Degenerate Sigma-2 with Unconnectedness 4 | 4 | Rectangle |
|  | Computing the maximal Boolean complexity of families of Aristotelian diagrams, p. 1334, by Demey, Lorenz | 2018 | Jacoby-Sesmat-Blanché Sigma-3 | 4 | Hexagon |
|  | Computing the maximal Boolean complexity of families of Aristotelian diagrams, p. 1334, by Demey, Lorenz | 2018 | Jacoby-Sesmat-Blanché Sigma-3 | 3 | Hexagon |
|  | Combinatorial Bitstring Semantics for Arbitrary Logical Fragments, p. 330, by Demey, Lorenz; Smessaert, Hans | 2018 | Classical Sigma-2 | 3 | Rectangle |