| 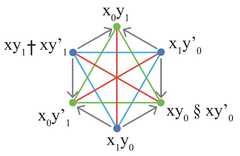 | Was Lewis Carroll an Amazing Oppositional Geometer?, p. 402, by Moretti, Alessio | 2014 | Jacoby-Sesmat-Blanché Sigma-3 | 4 | Hexagon |
|  | Was Lewis Carroll an Amazing Oppositional Geometer?, p. 402, by Moretti, Alessio | 2014 | Jacoby-Sesmat-Blanché Sigma-3 | 4 | Hexagon |
|  | Was Lewis Carroll an Amazing Oppositional Geometer?, p. 402, by Moretti, Alessio | 2014 | Jacoby-Sesmat-Blanché Sigma-3 | 4 | Hexagon |
|  | Was Lewis Carroll an Amazing Oppositional Geometer?, p. 402, by Moretti, Alessio | 2014 | Jacoby-Sesmat-Blanché Sigma-3 | 4 | Hexagon |
|  | Was Lewis Carroll an Amazing Oppositional Geometer?, p. 402, by Moretti, Alessio | 2014 | Jacoby-Sesmat-Blanché Sigma-3 | 4 | Hexagon |
| 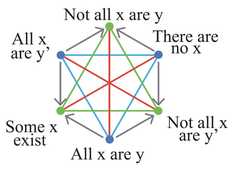 | Was Lewis Carroll an Amazing Oppositional Geometer?, p. 402, by Moretti, Alessio | 2014 | Jacoby-Sesmat-Blanché Sigma-3 | 4 | Hexagon |
|  | Was Lewis Carroll an Amazing Oppositional Geometer?, p. 402, by Moretti, Alessio | 2014 | Jacoby-Sesmat-Blanché Sigma-3 | 4 | Hexagon |
|  | Was Lewis Carroll an Amazing Oppositional Geometer?, p. 404, by Moretti, Alessio | 2014 | Jacoby-Sesmat-Blanché Sigma-3 | 3–4 | Hexagon |
|  | Was Lewis Carroll an Amazing Oppositional Geometer?, p. 404, by Moretti, Alessio | 2014 | Classical Sigma-7 | 4–5 | Tetrahedron |
|  | Was Lewis Carroll an Amazing Oppositional Geometer?, p. 404, by Moretti, Alessio | 2014 | Classical Sigma-7 | 4–5 | Rhombic Dodecahedron |
|  | Was Lewis Carroll an Amazing Oppositional Geometer?, p. 398, by Moretti, Alessio | 2014 | Classical Sigma-7 | 4 | Tetrahedron |
|  | Was Lewis Carroll an Amazing Oppositional Geometer?, p. 398, by Moretti, Alessio | 2014 | Classical Sigma-7 | 4 | Cube |
|  | Was Lewis Carroll an Amazing Oppositional Geometer?, p. 398, by Moretti, Alessio | 2014 | Classical Sigma-7 | 4 | Rhombic Dodecahedron |
| 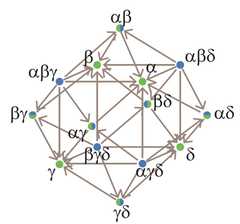 | Was Lewis Carroll an Amazing Oppositional Geometer?, p. 398, by Moretti, Alessio | 2014 | Classical Sigma-7 | 4 | Rhombic Dodecahedron |
| 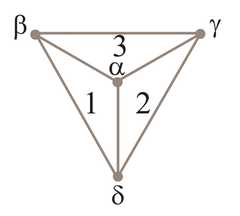 | Was Lewis Carroll an Amazing Oppositional Geometer?, p. 393, by Moretti, Alessio | 2014 | Subcontrariety 4-clique | 4 | Triangle |
|  | Was Lewis Carroll an Amazing Oppositional Geometer?, p. 393, by Moretti, Alessio | 2014 | Subcontrariety 4-clique | 4 | Triangle |
| 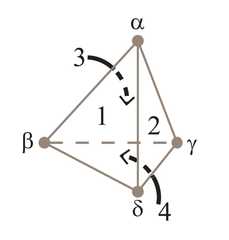 | Was Lewis Carroll an Amazing Oppositional Geometer?, p. 393, by Moretti, Alessio | 2014 | Subcontrariety 4-clique | 4 | Tetrahedron |
|  | Was Lewis Carroll an Amazing Oppositional Geometer?, p. 395, by Moretti, Alessio | 2014 | Classical Sigma-7 | 4–5 | Tetrahedron |
|  | Was Lewis Carroll an Amazing Oppositional Geometer?, p. 395, by Moretti, Alessio | 2014 | Classical Sigma-7 | 4–5 | Tetrahedron |
| 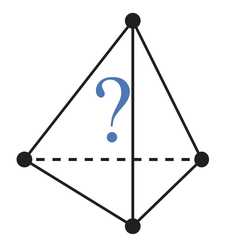 | Was Lewis Carroll an Amazing Oppositional Geometer?, p. 395, by Moretti, Alessio | 2014 | Contrariety 4-clique | 4–5 | Tetrahedron |
|  | Was Lewis Carroll an Amazing Oppositional Geometer?, p. 395, by Moretti, Alessio | 2014 | Subcontrariety 4-clique | 4–5 | Tetrahedron |
|  | Was Lewis Carroll an Amazing Oppositional Geometer?, p. 392, by Moretti, Alessio | 2014 | Classical Sigma-2 | 3 | Trapezoid |
|  | Was Lewis Carroll an Amazing Oppositional Geometer?, p. 392, by Moretti, Alessio | 2014 | Classical Sigma-2 | 3 | Trapezoid |
|  | Was Lewis Carroll an Amazing Oppositional Geometer?, p. 392, by Moretti, Alessio | 2014 | Classical Sigma-2 | 3 | Square |
|  | Was Lewis Carroll an Amazing Oppositional Geometer?, p. 392, by Moretti, Alessio | 2014 | Degenerate Sigma-2 with Unconnectedness 4 | 4 | Trapezoid |