How to Square Knowledge and Belief (2012), p. 310
by Lenzen, Wolfgang

Copyright according to our policy

Caption

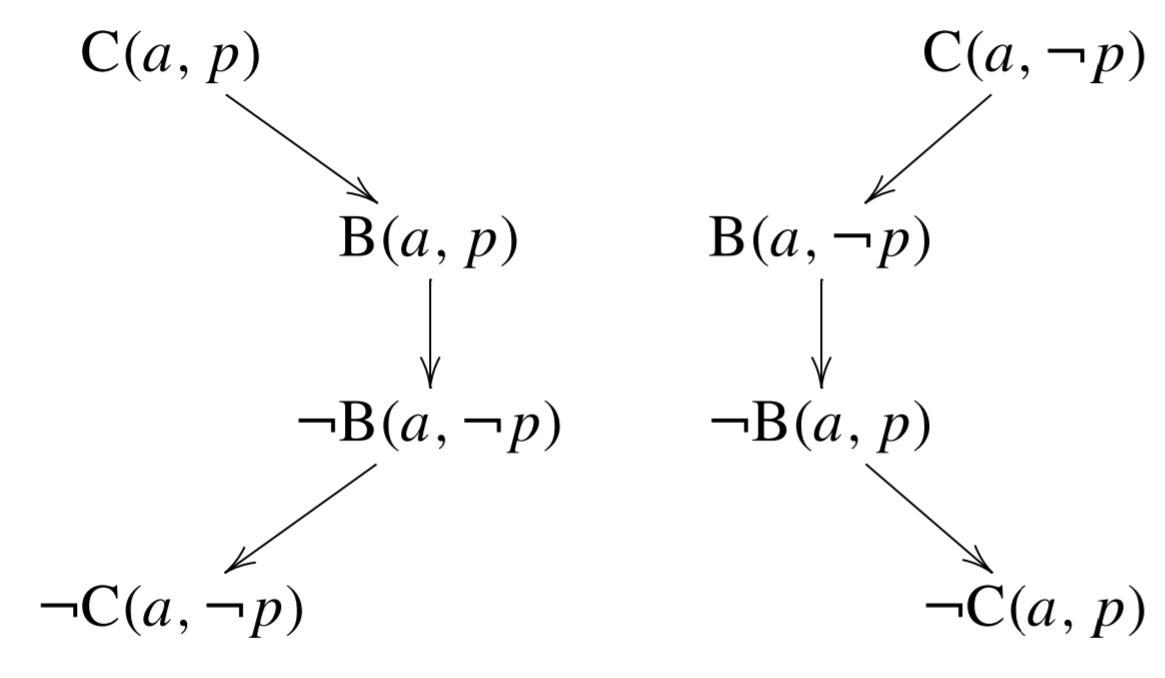
Doxastic square of opposition

Logic

Aristotelian family

Lenzen Sigma-4

Boolean complexity

5

Number of labels per vertex (at most)

1

Uniqueness of the vertices up to logical equivalence

Yes

Errors in the diagram

No

Geometry

Shape

Rectangle (irregular)

Colinearity range

0

Coplanarity range

2

Cospatiality range

0

Representation of contradiction

By central symmetry

Graph structure

$B(a,p)$

• Implicit contradiction with $\neg B(a,p)$
• Implicit contrariety with $C(a,\neg p)$
• Implicit contrariety with $B(a,\neg p)$
• Implicit subcontrariety with $\neg C(a,p)$
• Subalternation from $C(a,p)$
• Implicit subalternation to $\neg C(a,\neg p)$
• Subalternation to $\neg B(a,\neg p)$

$C(a,p)$

• Implicit contradiction with $\neg C(a,p)$
• Implicit contrariety with $\neg B(a,p)$
• Implicit contrariety with $C(a,\neg p)$
• Implicit contrariety with $B(a,\neg p)$
• Subalternation to $B(a,p)$
• Implicit subalternation to $\neg C(a,\neg p)$
• Implicit subalternation to $\neg B(a,\neg p)$

$\neg C(a,\neg p)$

• Implicit contradiction with $C(a,\neg p)$
• Implicit subcontrariety with $B(a,\neg p)$
• Implicit subcontrariety with $\neg B(a,p)$
• Implicit subcontrariety with $\neg C(a,p)$
• Implicit subalternation from $C(a,p)$
• Implicit subalternation from $B(a,p)$
• Subalternation from $\neg B(a,\neg p)$

$\neg C(a,p)$

• Implicit contradiction with $C(a,p)$
• Implicit subcontrariety with $B(a,p)$
• Implicit subcontrariety with $\neg B(a,\neg p)$
• Implicit subcontrariety with $\neg C(a,\neg p)$
• Implicit subalternation from $C(a,\neg p)$
• Subalternation from $\neg B(a,p)$
• Implicit subalternation from $B(a,\neg p)$

$B(a,\neg p)$

• Implicit contradiction with $\neg B(a,\neg p)$
• Implicit contrariety with $B(a,p)$
• Implicit contrariety with $C(a,p)$
• Implicit subcontrariety with $\neg C(a,\neg p)$
• Subalternation from $C(a,\neg p)$
• Subalternation to $\neg B(a,p)$
• Implicit subalternation to $\neg C(a,p)$

$\neg B(a,p)$

• Implicit contradiction with $B(a,p)$
• Implicit contrariety with $C(a,p)$
• Implicit subcontrariety with $\neg B(a,\neg p)$
• Implicit subcontrariety with $\neg C(a,\neg p)$
• Subalternation from $B(a,\neg p)$
• Implicit subalternation from $C(a,\neg p)$
• Subalternation to $\neg C(a,p)$

$\neg B(a,\neg p)$

• Implicit contradiction with $B(a,\neg p)$
• Implicit contrariety with $C(a,\neg p)$
• Implicit subcontrariety with $\neg C(a,p)$
• Implicit subcontrariety with $\neg B(a,p)$
• Subalternation from $B(a,p)$
• Implicit subalternation from $C(a,p)$
• Subalternation to $\neg C(a,\neg p)$

$C(a,\neg p)$

• Implicit contradiction with $\neg C(a,\neg p)$
• Implicit contrariety with $C(a,p)$
• Implicit contrariety with $B(a,p)$
• Implicit contrariety with $\neg B(a,\neg p)$
• Implicit subalternation to $\neg B(a,p)$
• Implicit subalternation to $\neg C(a,p)$
• Subalternation to $B(a,\neg p)$

Vertex description

Conceptual info

No

Mnemonic support (AEIO, purpurea ...)

No

Form

none

Label type

symbolic

Symbolic field

logic

Contains partial formulas or symbols

No

Logical system

epistemic logic

Edge description

Contains definitions of relations

No

Form

solid lines

,

none

Has arrowheads

Yes

Overlap

No

Curved

No

Hooked

No

As wide as vertices

No

Contains text

No

Label type

none

Style

Diagram is colored

No

Diagram is embellished

No