Not Only Barbara (2015), p. 101
by Dekker, Paul
Copyright according to our policy
- Aristotelian family
- Moretti-Pellissier Sigma-4
- Boolean complexity
- 5
- Number of labels per vertex (at most)
- 1
- Uniqueness of the vertices up to logical equivalence
- Yes
- Errors in the diagram
- No
- Shape
- Cube (regular)
- Colinearity range
- 0
- Coplanarity range
- 0
- Cospatiality range
- 0
- Representation of contradiction
- By some other geometric feature
Logic
Geometry
- Conceptual info
- Yes
- Mnemonic support (AEIO, purpurea ...)
- Yes
- Form
- none
- Label type
- symbolic
- Symbolic field
- logic
- Contains partial formulas or symbols
- Yes
- Logical system
- syllogistics
- Contains definitions of relations
- No
- Form
- solid lines ,
- none
- Has arrowheads
- No
- Overlap
- No
- Curved
- No
- Hooked
- No
- As wide as vertices
- No
- Contains text
- No
- Label type
- none
Vertex description
Edge description
- Diagram is colored
- No
- Diagram is embellished
- No
- Tags
- subject negation ;
- generalized Post duality
Style
Additional notes
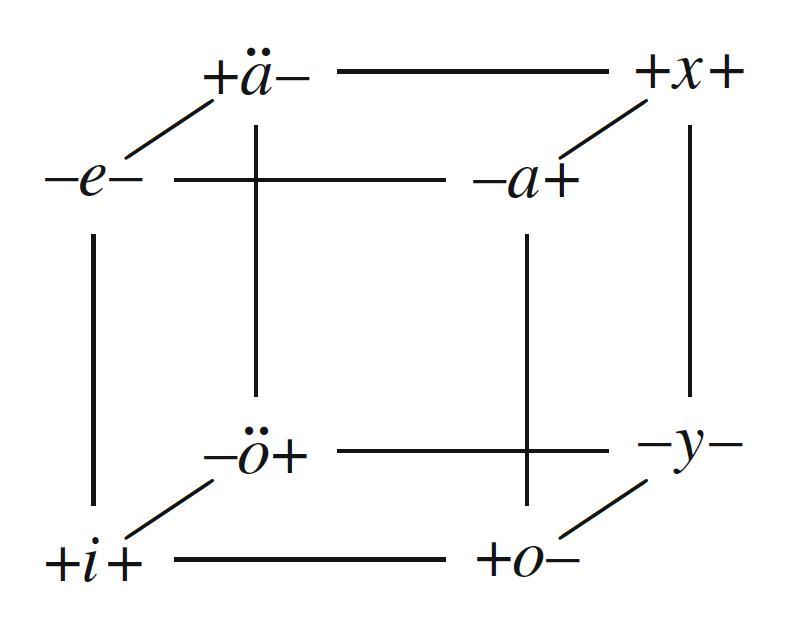
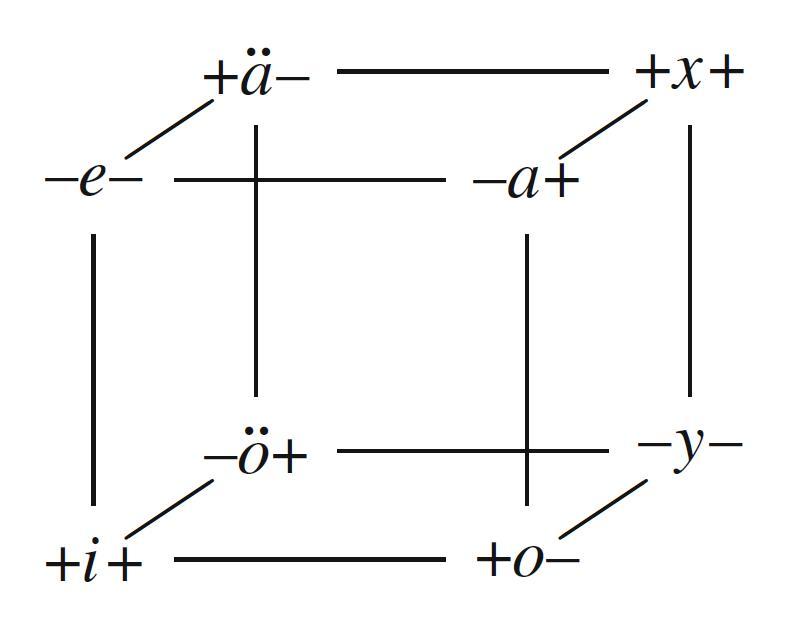
- AäB = A'eB = $\forall x(\neg Ax \to \neg Bx)$
AxB = A'aB = $\forall x(\neg Ax \to Bx)$
AöB = A'iB = $\exists x(\neg Ax \wedge Bx)$
AyB = A'oB = $\exists x(\neg Ax \wedge \neg Bx)$
(Cf. p. 99.)
The $+$ and $-$ indicate monotonicity entailment patterns for the subject and predicate position.
This is a Moretti sigma-4 (rather than a Keynes-Johnson sigma-4), because we assume not only existential import, but also 'differential import': "The $\textit{differential import}$ of a proposition AuB is that A and B make a different proper distinction, i.e., $A \neq \emptyset \neq A'$, $B \neq \emptyset \neq B'$ and $A \neq B \neq A'$." (p. 100)
The partition induced by this diagram (subject to existential as well as differential import) consists of the following five anchor formulas:
$\bullet$ AaB
$\bullet$ AäB
$\bullet$ AeB
$\bullet$ AxB
$\bullet$ AiB $\wedge$ AoB $\wedge$ AöB $\wedge$ AyB