Traité de Logique Formelle (1930), p. 169
by Tricot, Jules

Copyright according to our policy
- Aristotelian family
- Buridan Sigma-4
- Boolean complexity
- 6
- Number of labels per vertex (at most)
- 1
- Uniqueness of the vertices up to logical equivalence
- Yes
- Errors in the diagram
- No
- Shape
- Octagon (irregular)
- Colinearity range
- 0
- Coplanarity range
- 0
- Cospatiality range
- 0
- Representation of contradiction
- By some other geometric feature
Logic
Geometry
- Conceptual info
- No
- Mnemonic support (AEIO, purpurea ...)
- Yes
- Form
- dots
- Label type
- linguistic
- Language
- Latin
- Lexical field
- modal syllogistics
- Contains partial sentences or single words
- Yes
- Contains abbreviations
- No
- Contains definitions of relations
- No
- Form
- none ,
- dashed lines
- Has arrowheads
- No
- Overlap
- No
- Curved
- No
- Hooked
- No
- As wide as vertices
- No
- Contains text
- Yes
- Label type
- linguistic ,
- none
- Language
- French
- Contains partial sentences or single words
- Yes
- Contain abbreviations
- No
Vertex description
Edge description
- Diagram is colored
- No
- Diagram is embellished
- No
Style
Additional notes
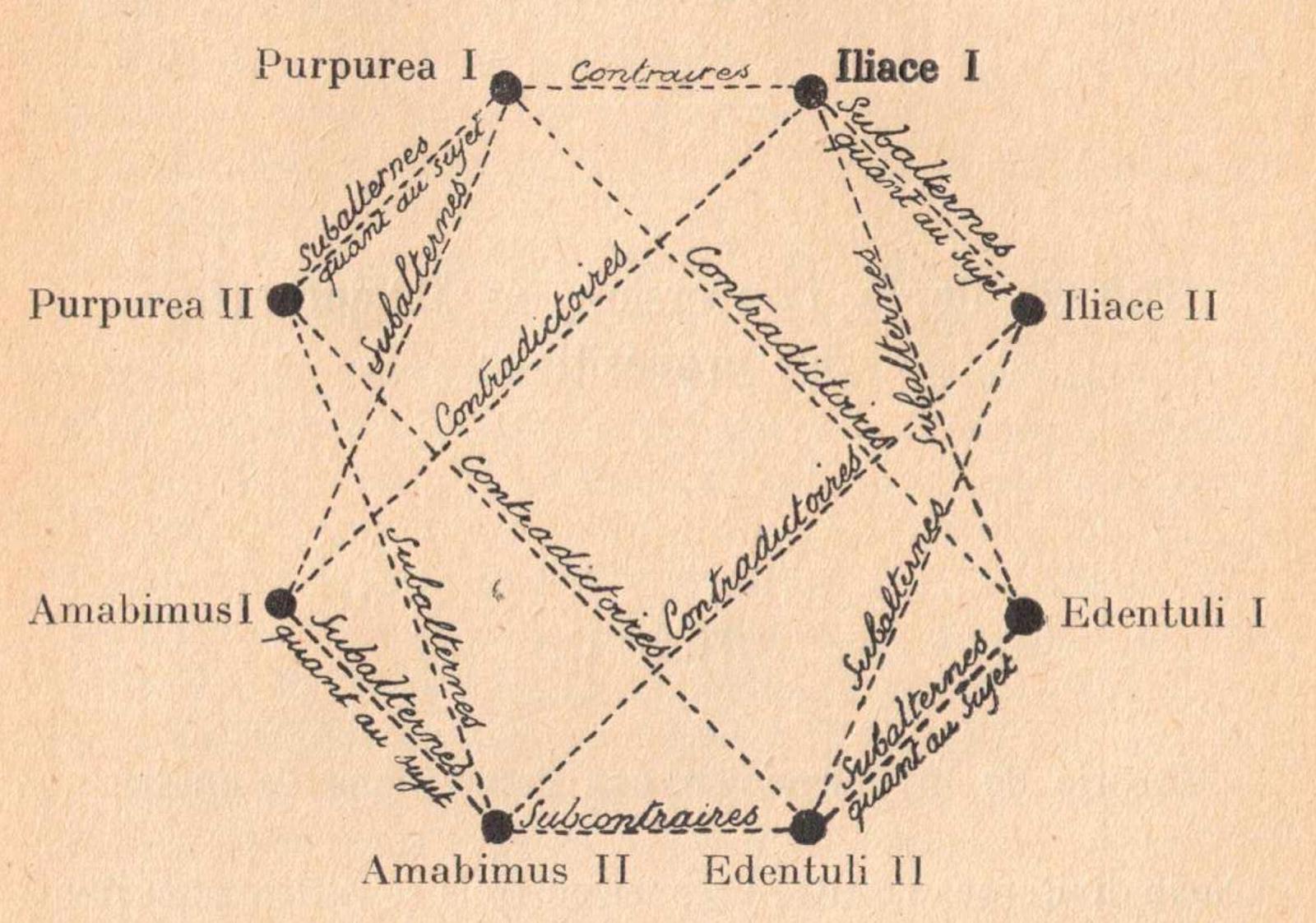
- The vertices contain de dicto quantified modal statements. I and II stand for a universal and existential quantifier, respectively.
Examples:
$\circ$ Purpurea I = it is necessary that all S are P
$\circ$ Purpurea II = it is necessary that some S are P
$\circ$ Amabimus I = it is possible that all S are P
$\circ$ Amabimus II = it is possible that some S are P
(Cf. pp. 168-169.)