The Logic of Future Contingents (2003), p. 219
by Shields, George W.; Viney, Donald W.

Copyright according to our policy
- Aristotelian family
- Classical Sigma-2
- Boolean complexity
- 3
- Number of labels per vertex (at most)
- 2
- Equivalence between (some) labels of the same vertex
- No
- Analogy between (some) labels of the same vertex
- No
- Uniqueness of the vertices up to logical equivalence
- Yes
- Errors in the diagram
- No
- Shape
- Rectangle (irregular)
- Colinearity range
- 0
- Coplanarity range
- 0
- Cospatiality range
- 0
- Representation of contradiction
- By central symmetry
Logic
Geometry
- Conceptual info
- No
- Mnemonic support (AEIO, purpurea ...)
- Yes
- Form
- none
- Label type
- symbolic
- Symbolic field
- logic
- Contains partial formulas or symbols
- Yes
- Logical system
- syllogistics ,
- predicate logic
- Contains definitions of relations
- No
- Form
- solid lines ,
- none
- Has arrowheads
- Yes
- Overlap
- No
- Curved
- No
- Hooked
- No
- As wide as vertices
- No
- Contains text
- No
- Label type
- none
Vertex description
Edge description
- Diagram is colored
- No
- Diagram is embellished
- No
Style
Additional notes
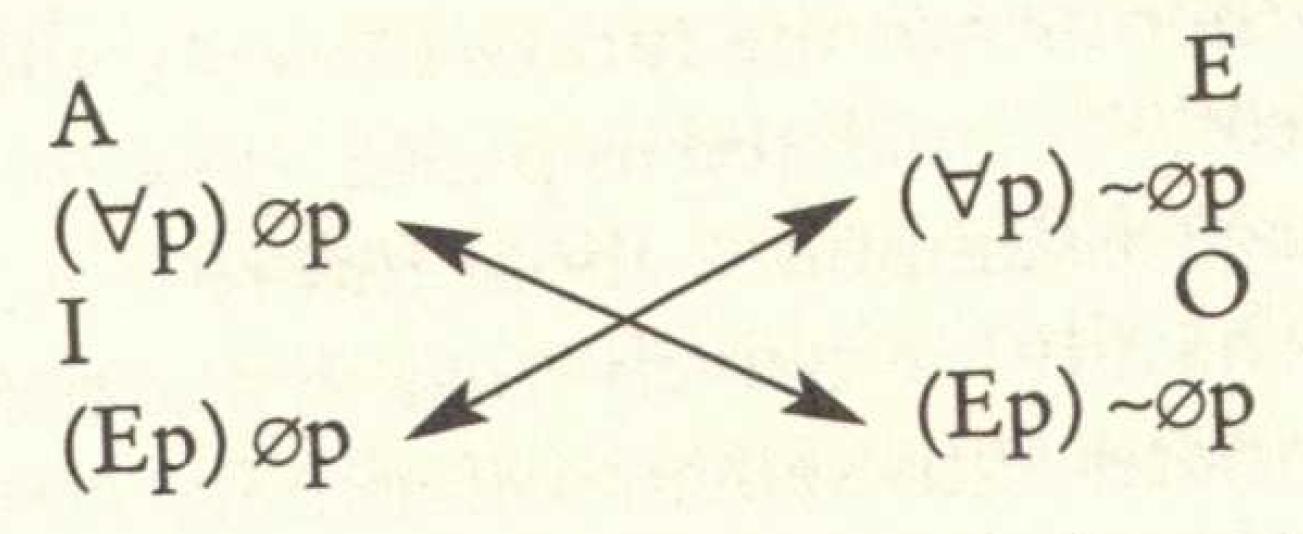
- $(\forall p)\phi p$: All causal conditions at t are such that e is going to occur.
$(\forall p)\sim\phi p$: All causal conditions at t are such that it is not the case that e is going to occur.
$(E p)\phi p$: There is at least one causal condition at t such that e is going to occur.
$(E p)\sim\phi p$: There is at least one causal condition at t such that it is not the case that e is going to occur.
(Cf. p. 219.)