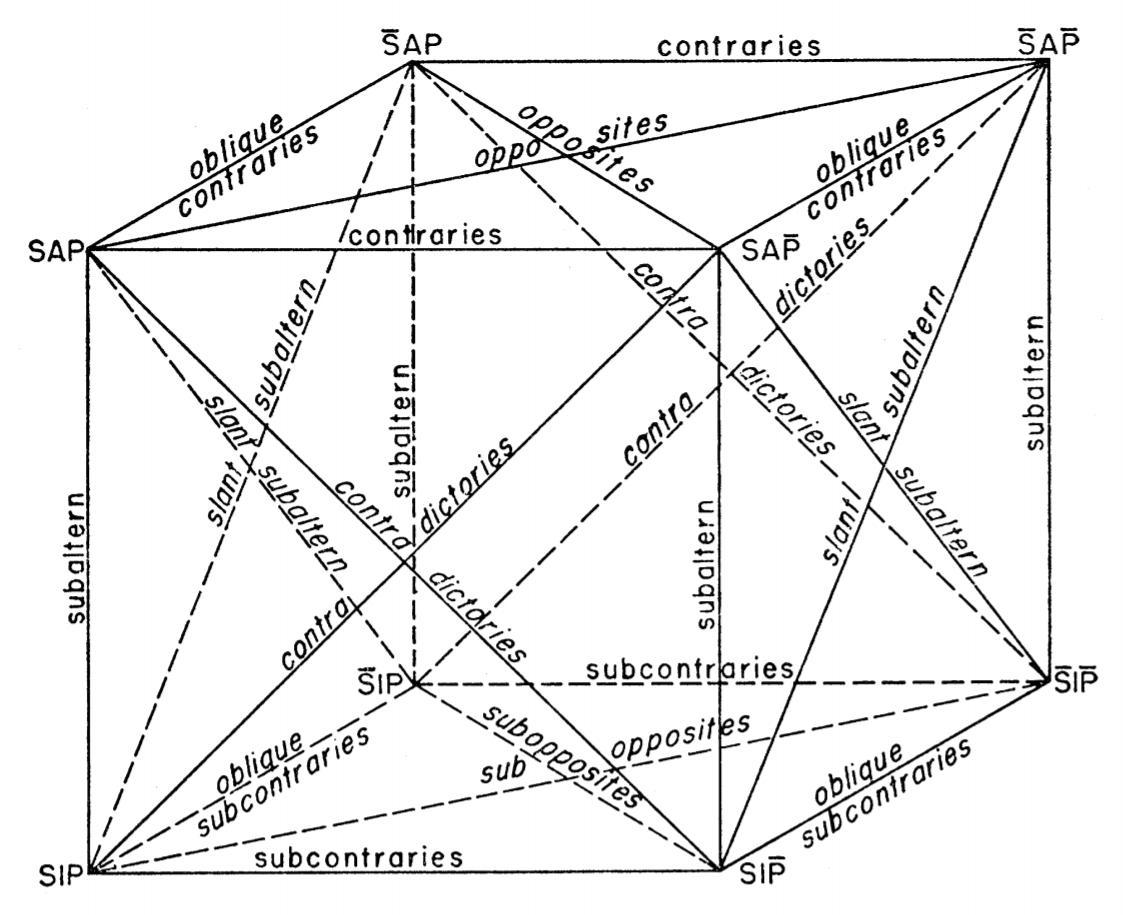
The Syllogism Revised (1952), p. 4
by Reichenbach, Hans
Copyright according to our policy
Caption
- CUBE OF OPPOSITION
- Aristotelian family
- Moretti-Pellissier Sigma-4
- Boolean complexity
- 5
- Number of labels per vertex (at most)
- 1
- Uniqueness of the vertices up to logical equivalence
- Yes
- Errors in the diagram
- No
- Shape
- Cube (regular)
- Colinearity range
- 0
- Coplanarity range
- 0
- Cospatiality range
- 0
- Representation of contradiction
- By some other geometric feature
Logic
Geometry
- Conceptual info
- No
- Mnemonic support (AEIO, purpurea ...)
- Yes
- Form
- none
- Label type
- symbolic
- Symbolic field
- logic
- Contains partial formulas or symbols
- No
- Logical system
- syllogistics
- Contains definitions of relations
- No
- Form
- solid lines ,
- none ,
- dashed lines
- Has arrowheads
- No
- Overlap
- No
- Curved
- No
- Hooked
- No
- As wide as vertices
- No
- Contains text
- Yes
- Label type
- linguistic
- Language
- English
- Contains partial sentences or single words
- Yes
- Contain abbreviations
- No
Vertex description
Edge description
- Diagram is colored
- No
- Diagram is embellished
- No
- Tags
- subject negation ;
- generalized Post duality
Style
Additional notes
- This diagram contains the 8 formulas of syllogistics with subject negation. Usually, these formulas are used to construct a Keynes-Johnson sigma-4, based on four existential import assumptions (viz.: there is at least one S, at least one non-S, at least one P, at least one non-P). However, Reichenbach additionally makes two 'differential import' assumptions (viz.: S is distinct from P, S is distinct from non-P), thus obtaining a Moretti-Pellissier sigma-4.