From Analogical Proportion to Logical Proportions (2013), p. 480
by Prade, Henri; Richard, Gilles
Copyright according to our policy
Caption
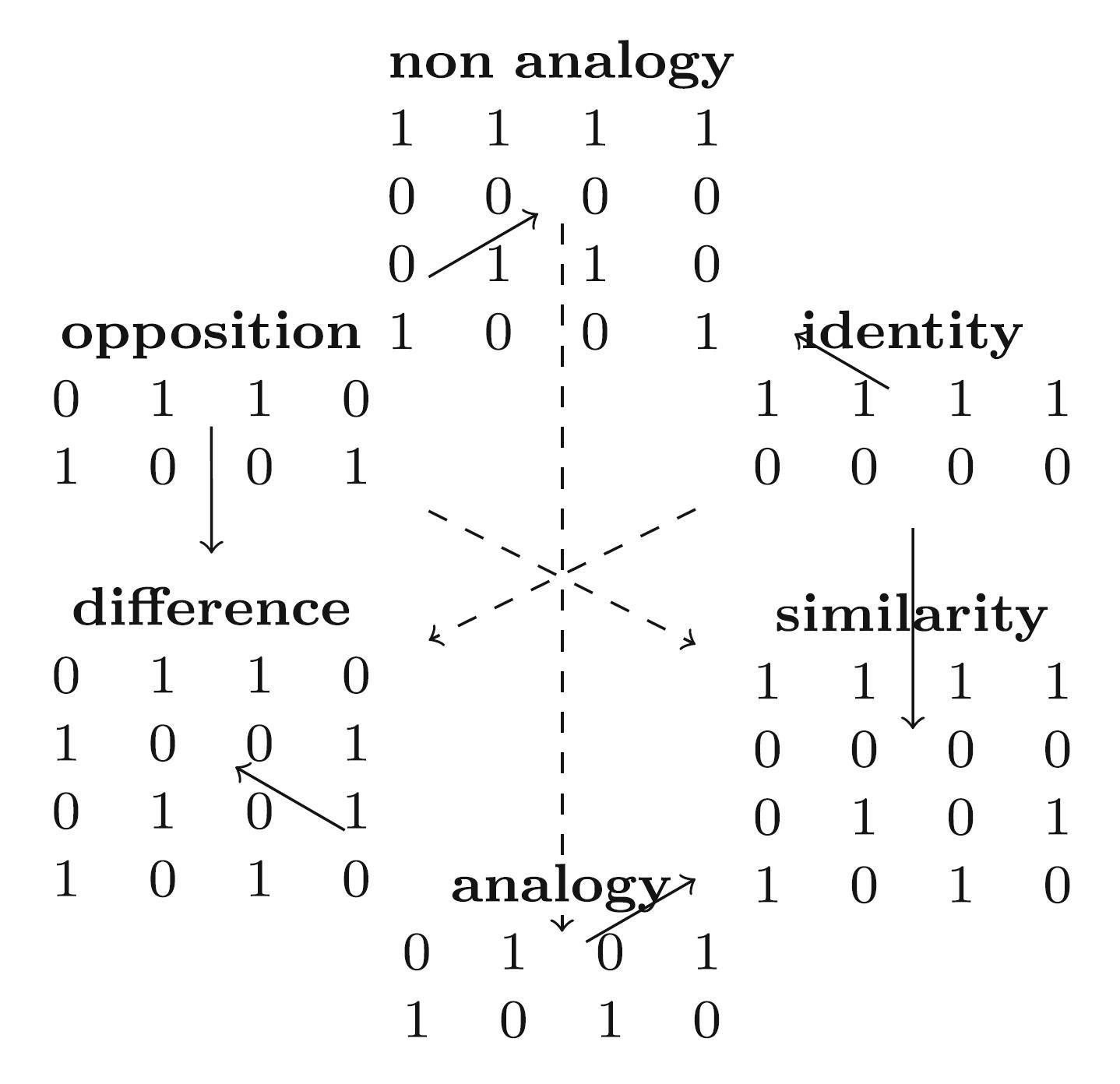
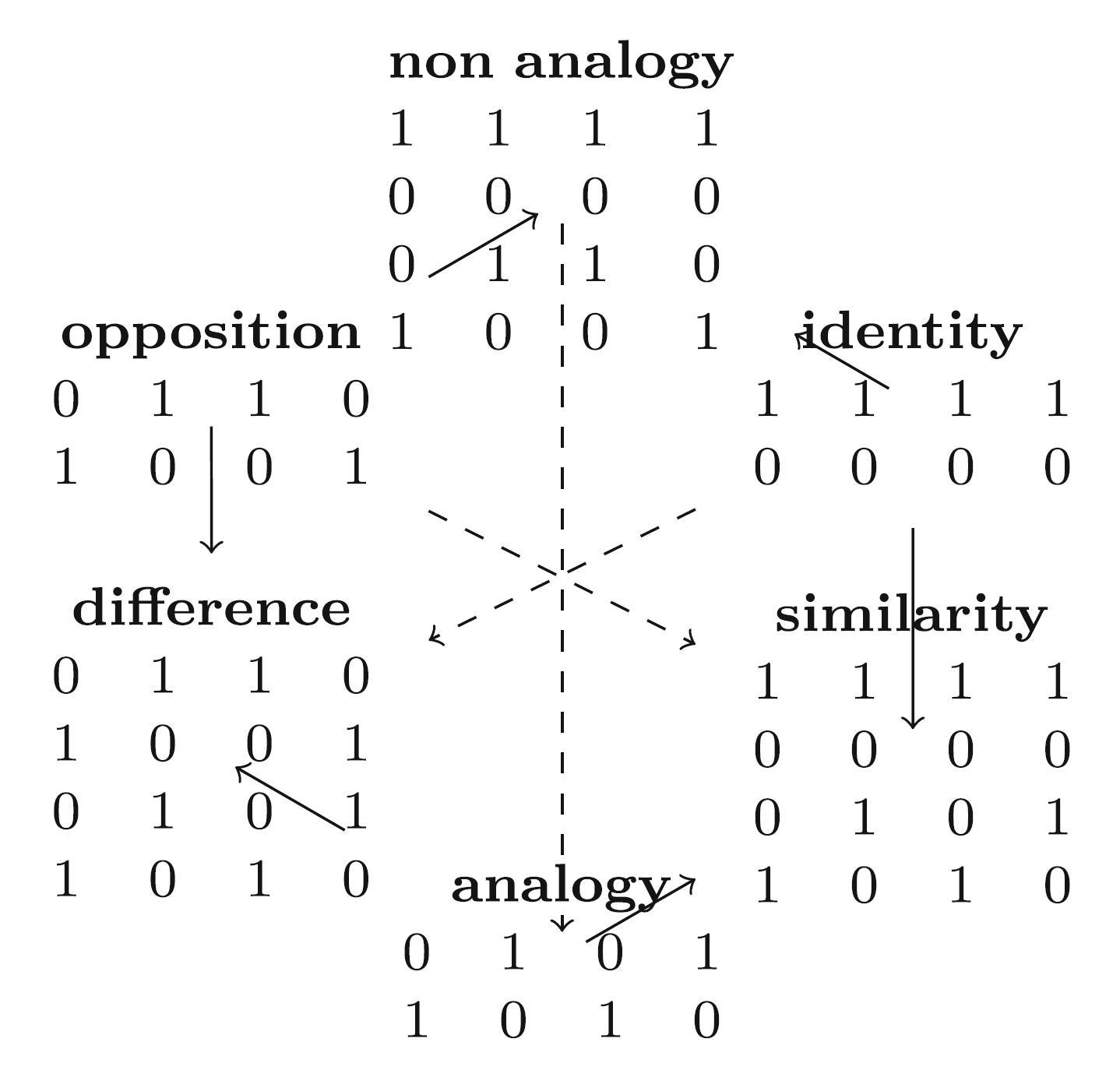
- Moretti’s and Béziau’s hexagons induced by decomposing analogy and paralogy truth tables. The hexagons show the patterns for which the corresponding vertices are true
- Aristotelian family
- Jacoby-Sesmat-Blanché Sigma-3
- Boolean complexity
- 3
- Number of labels per vertex (at most)
- 2
- Equivalence between (some) labels of the same vertex
- No
- Analogy between (some) labels of the same vertex
- No
- Uniqueness of the vertices up to logical equivalence
- Yes
- Errors in the diagram
- No
- Shape
- Hexagon (regular)
- Colinearity range
- 0
- Coplanarity range
- 0
- Cospatiality range
- 0
- Representation of contradiction
- By central symmetry
Logic
Geometry
- Conceptual info
- No
- Mnemonic support (AEIO, purpurea ...)
- No
- Form
- none
- Label type
- linguistic ,
- symbolic
- Language
- English
- Lexical field
- nouns
- Contains partial sentences or single words
- Yes
- Contains abbreviations
- No
- Symbolic field
- mathematics
- Contains partial formulas or symbols
- No
- Mathematical branch
- set theory
- Contains definitions of relations
- No
- Form
- solid lines ,
- none ,
- dashed lines
- Has arrowheads
- Yes
- Overlap
- No
- Curved
- No
- Hooked
- No
- As wide as vertices
- No
- Contains text
- No
- Label type
- none
Vertex description
Edge description
- Diagram is colored
- No
- Diagram is embellished
- No
- Tags
- Boolean closed
Style
Additional notes
- The vertices of this diagram are occupied by subsets of $\{1111, 0000, 1001, 0110, 1010, 0101\}$.