Probabilistic squares and hexagons of opposition under coherence (2017), p. 290
by Pfeifer, Niki; Sanfilippo, Giuseppe
Copyright according to our policy
Caption
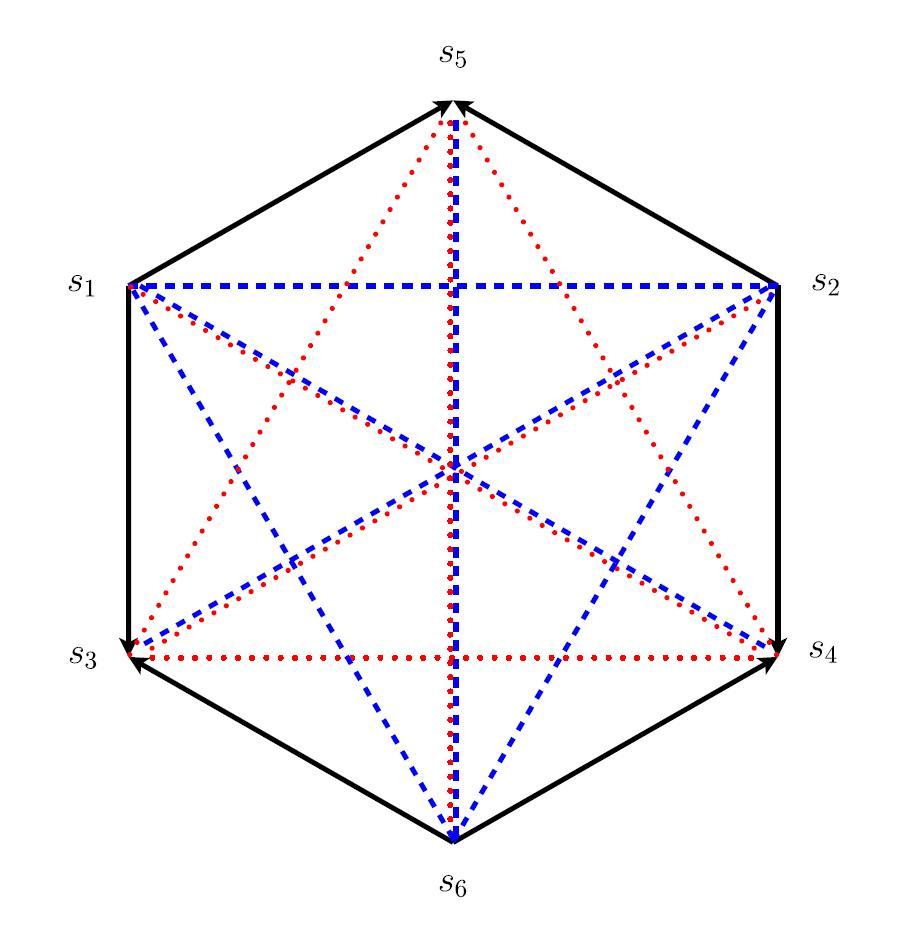
- Probabilistic hexagon of opposition defined on the six sentence types $(s_1, s_2, s_3, s_4, s_5, s_6)$, where $(s_1, s_2, s_3, s_4)$ is a square of opposition, $s_5 = s_1 \vee s_2$, and $s_6 = s_3 \wedge s_4$ (see Definition 12). The arrows indicate subalternation, dashed lines indicate contraries, and dotted lines indicate sub-contraries. Contradictories are indicated by combined dotted and dashed lines.
- Aristotelian family
- Jacoby-Sesmat-Blanché Sigma-3
- Boolean complexity
- 3
- Number of labels per vertex (at most)
- 1
- Uniqueness of the vertices up to logical equivalence
- Yes
- Errors in the diagram
- No
- Shape
- Hexagon (regular)
- Colinearity range
- 0
- Coplanarity range
- 0
- Cospatiality range
- 0
- Representation of contradiction
- By central symmetry
Logic
Geometry
- Conceptual info
- No
- Mnemonic support (AEIO, purpurea ...)
- No
- Form
- none
- Label type
- generic placeholders
Vertex description
Edge description
- Diagram is colored
- Yes
- Diagram is embellished
- No
- Tags
- Boolean closed
Style
Additional notes
- On p. 290 it is stated that $s_5 = s_1 \vee s_2$ and $s_6 = \overline{s}_1 \wedge \overline{s}_2 = s_4 \wedge s_3$. Hence, this diagram is a strong JSB hexagon (with Boolean complexity 3).