Probabilistic squares and hexagons of opposition under coherence (2017), p. 289
by Pfeifer, Niki; Sanfilippo, Giuseppe

Copyright according to our policy

Caption

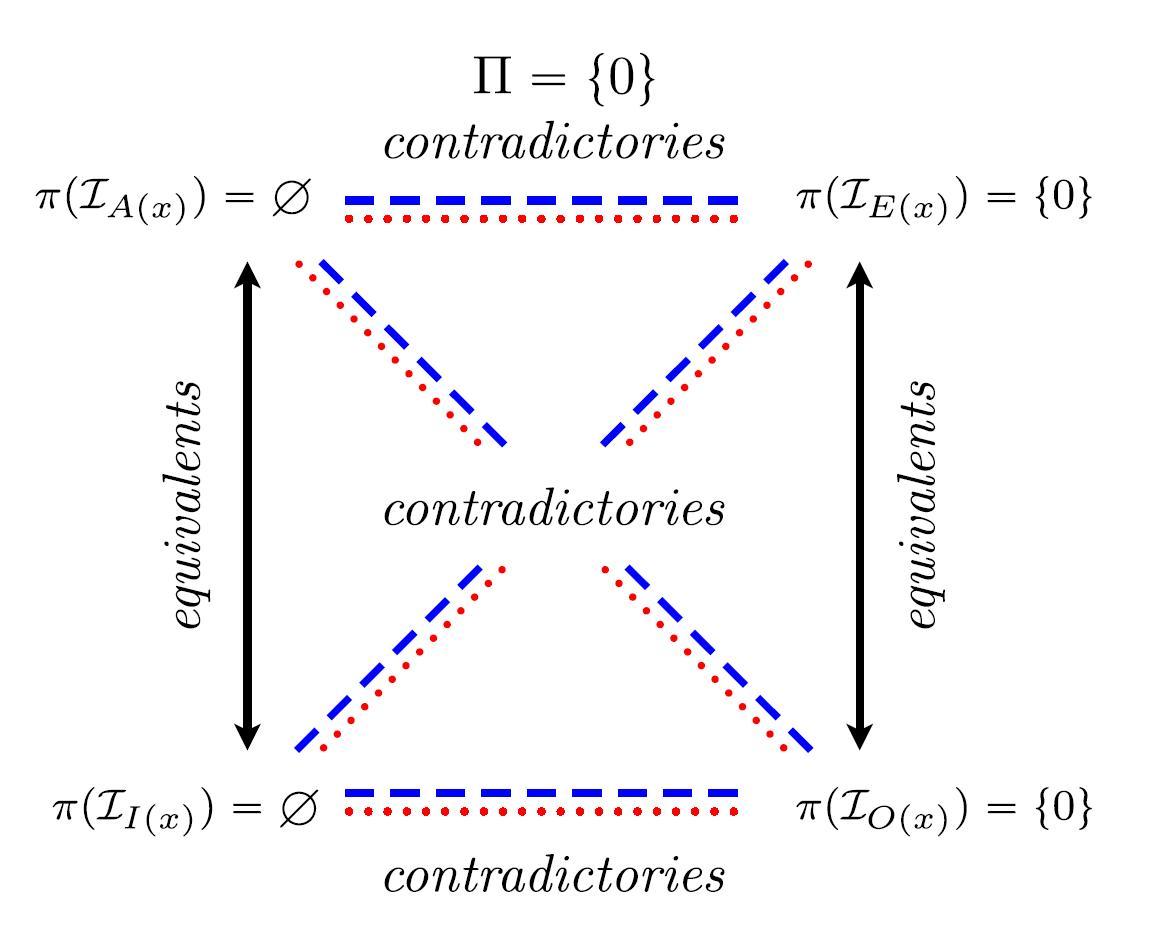
Degenerated squares of opposition $(\pi(\mathcal{I}_{A(x)}), \pi(\mathcal{I}_{E(x)}), \pi(\mathcal{I}_{I(x)}), \pi(\mathcal{I}_{O(x)})$ when $\mathcal{F}$ consists of the conditional event $P|S$ and the set of all coherent assessments on $P|S$ is $\Pi = \{1\}$ (i.e., $P\wedge S=S$; left) or $\Pi = \{0\}$ (i.e., $P\wedge S=\bot$; right).

Logic

Aristotelian family

A Single PCD

Boolean complexity

2

Number of labels per vertex (at most)

1

Uniqueness of the vertices up to logical equivalence

No

Errors in the diagram

No

Geometry

Shape

Square (regular)

Colinearity range

0

Coplanarity range

0

Cospatiality range

0

Representation of contradiction

By central symmetry

Vertex description

Conceptual info

No

Mnemonic support (AEIO, purpurea ...)

Yes

Form

none

Label type

symbolic

Symbolic field

mathematics

Contains partial formulas or symbols

No

Mathematical branch

probability theory

Edge description

Style

Diagram is colored

Yes

Diagram is embellished

No

Tags

Boolean closed