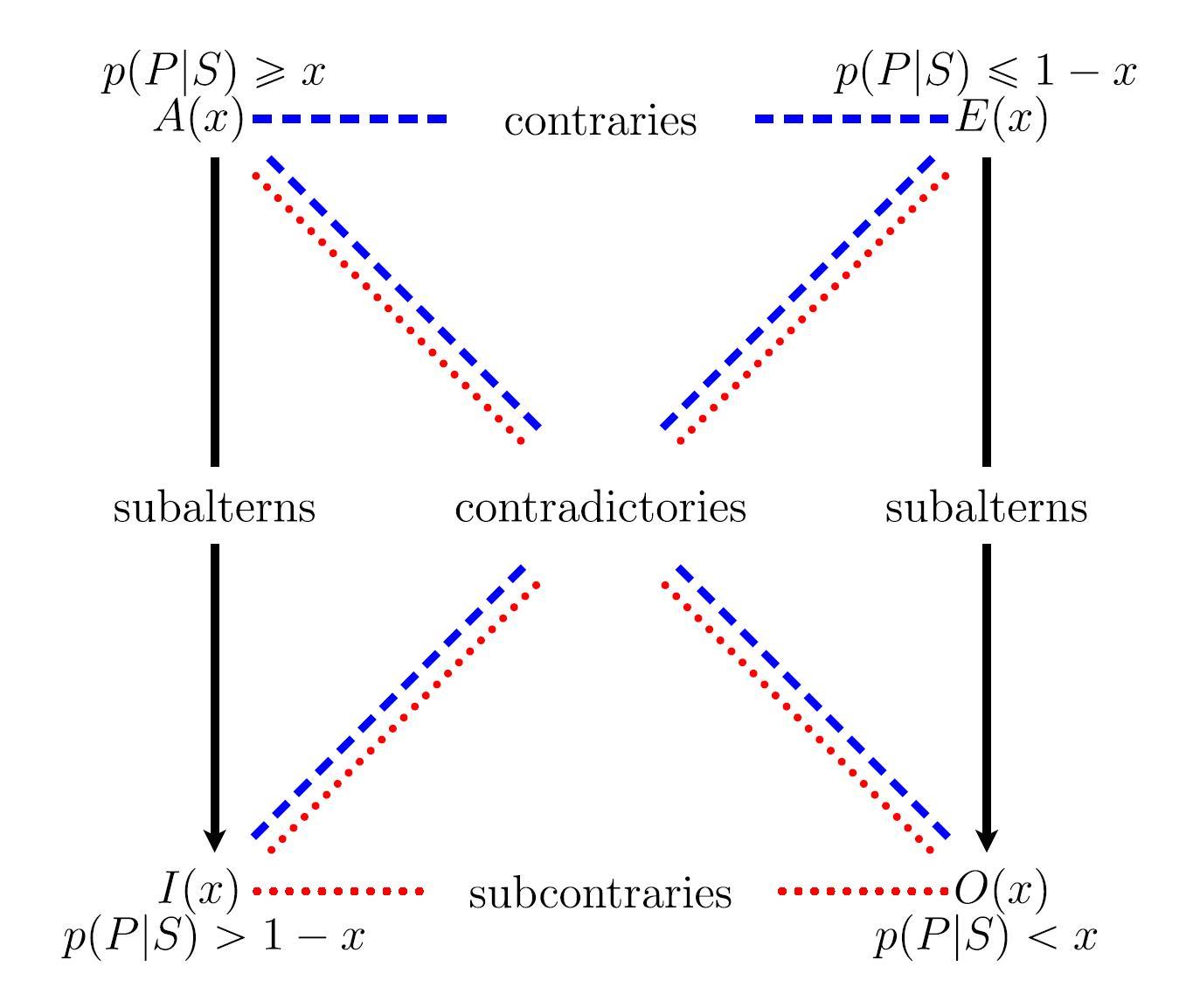
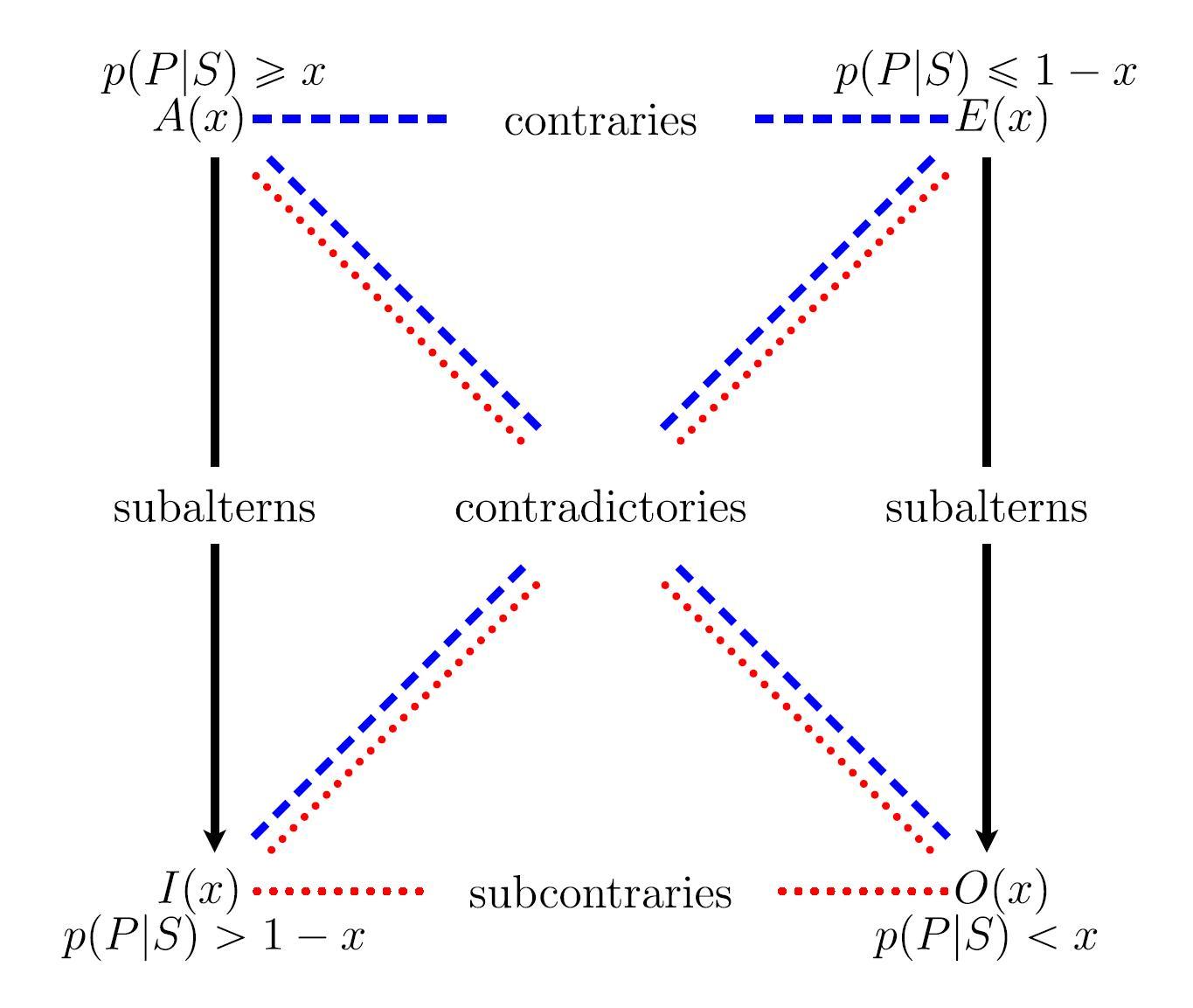
Probabilistic squares and hexagons of opposition under coherence (2017), p. 288
by Pfeifer, Niki; Sanfilippo, Giuseppe

Copyright according to our policy

Caption

Probabilistic square of opposition $\mathbf{S}(x)$ involving generalized quantifiers defined on the four sentence types ($A(x), E(x), I(x), O(x)$) with the threshold $x \in \, ]\frac{1}{2}, 1]$ (see also Table 1). In the extreme case where $x =1$, we obtain a new interpretation of the traditional square of opposition (see also Fig. 1), where the corners are labelled by "Every S is P" (A), "No S is P" (E), "Some S is P" (I), and "Some S is not P" (O).

Logic

Aristotelian family

Classical Sigma-2

Boolean complexity

3

Number of labels per vertex (at most)

2

Equivalence between (some) labels of the same vertex

No

Analogy between (some) labels of the same vertex

No

Uniqueness of the vertices up to logical equivalence

Yes

Errors in the diagram

No

Geometry

Shape

Square (regular)

Colinearity range

0

Coplanarity range

0

Cospatiality range

0

Representation of contradiction

By central symmetry

Vertex description

Conceptual info

No

Mnemonic support (AEIO, purpurea ...)

Yes

Form

none

Label type

symbolic

Symbolic field

mathematics

,

logic

Contains partial formulas or symbols

Yes

Logical system

syllogistics

Mathematical branch

probability theory

Edge description

Style

Diagram is colored

Yes

Diagram is embellished

No