Aristotelian Logic (1991), p. 172
by Parry, William T.; Hacker, Edward A.
Copyright according to our policy
Caption
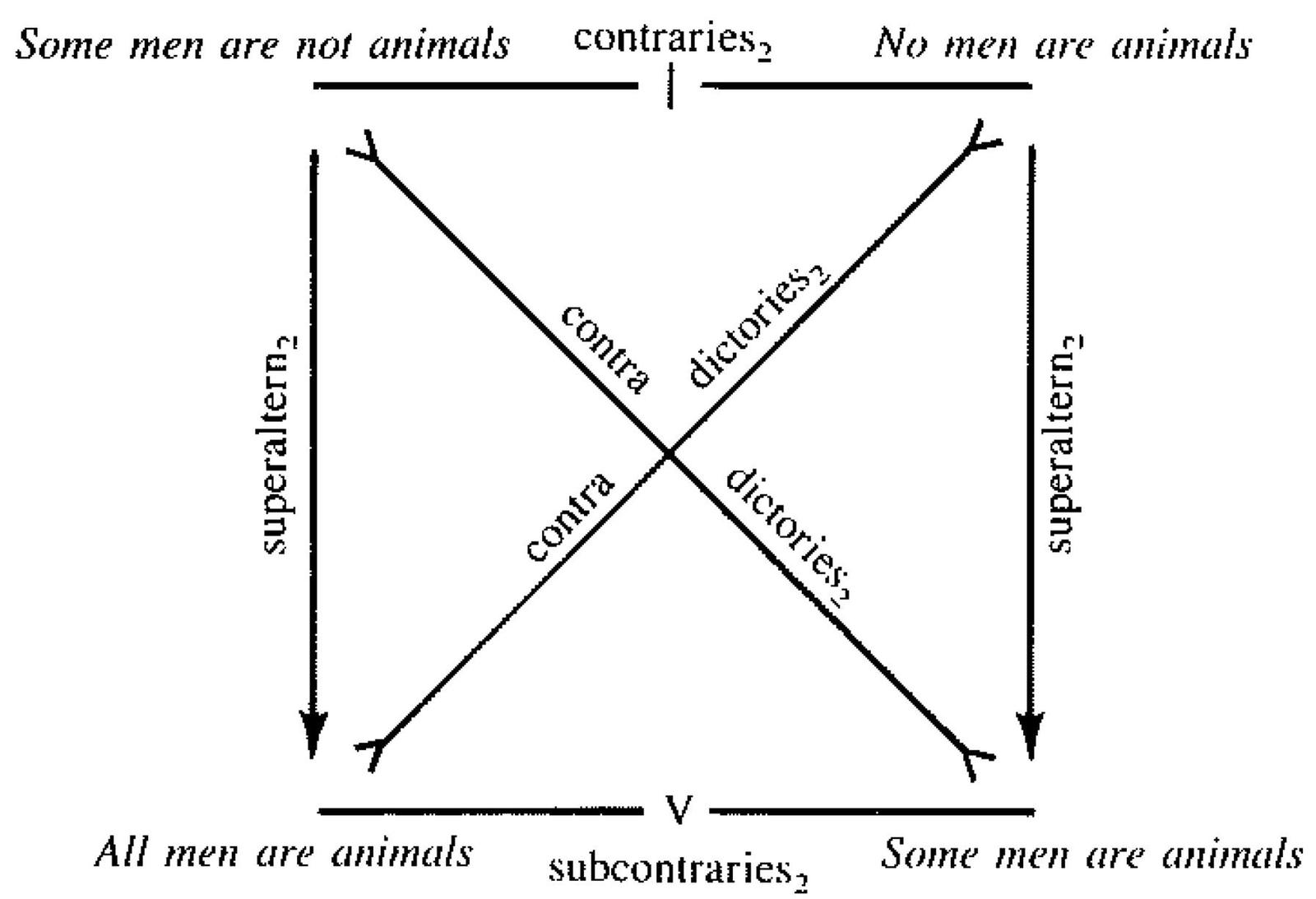
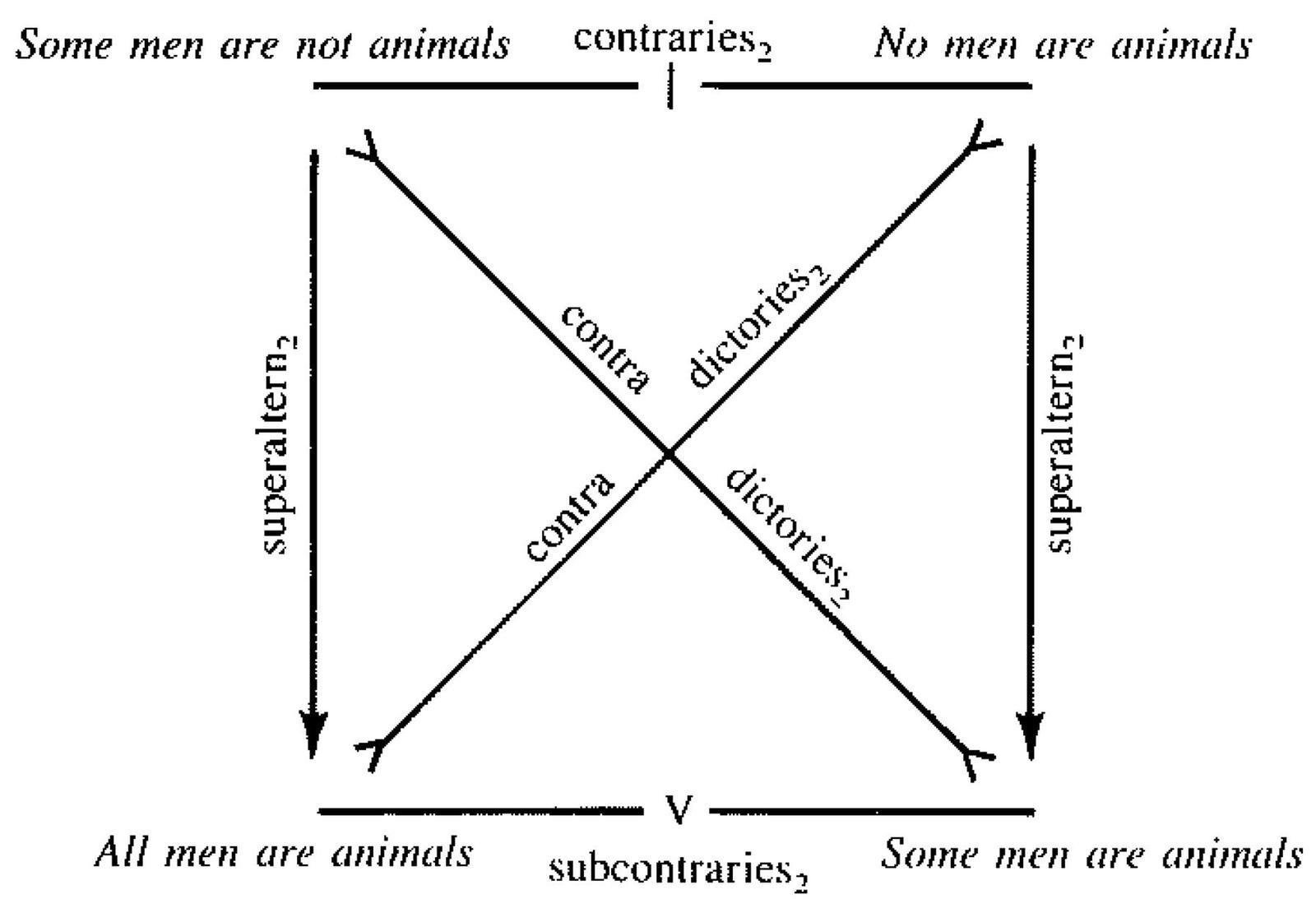
- "Modern" Square of Opposition for A priori Categoricals
- Aristotelian family
- Sigma-0 Graph
- Boolean complexity
- 1
- Number of labels per vertex (at most)
- 1
- Uniqueness of the vertices up to logical equivalence
- Yes
- Errors in the diagram
- Yes
- Shape
- Square (regular)
- Colinearity range
- 0
- Coplanarity range
- 0
- Cospatiality range
- 0
- Representation of contradiction
- By central symmetry
Logic
Geometry
- Conceptual info
- No
- Mnemonic support (AEIO, purpurea ...)
- No
- Form
- none
- Label type
- linguistic
- Language
- English
- Lexical field
- categorical
- Contains partial sentences or single words
- No
- Contains abbreviations
- No
- Contains definitions of relations
- No
- Form
- solid lines
- Has arrowheads
- Yes
- Overlap
- No
- Curved
- No
- Hooked
- No
- As wide as vertices
- No
- Contains text
- Yes
- Label type
- linguistic ,
- symbolic
- Language
- English
- Contains partial sentences or single words
- Yes
- Contain abbreviations
- No
- Symbolic field
- logic
- Contains partial formulas or symbols
- Yes
- Logical system
- propositional logic
Vertex description
Edge description
- Diagram is colored
- No
- Diagram is embellished
- No
- Tags
- Boolean closed ;
- non-contingent formulas
Style
Additional notes
- 'All men are animals' and 'Some men are animals' are tautological (under the assumption of existential import), while 'No men are animals' and 'Some men are not animals' are contradictory (under that same assumption). Hence this diagram contains only non-contingent formulas, and is thus a sigma-0 diagram.
The edges are labeled with propositional connectives corresponding to the Aristotelian relations (cf. Theorem 1 of Smessaert & Demey, 2014, Logical Geometries and Information in the Square of Oppositions, Journal of Logic, Language and Information 23 : 527 - 565).