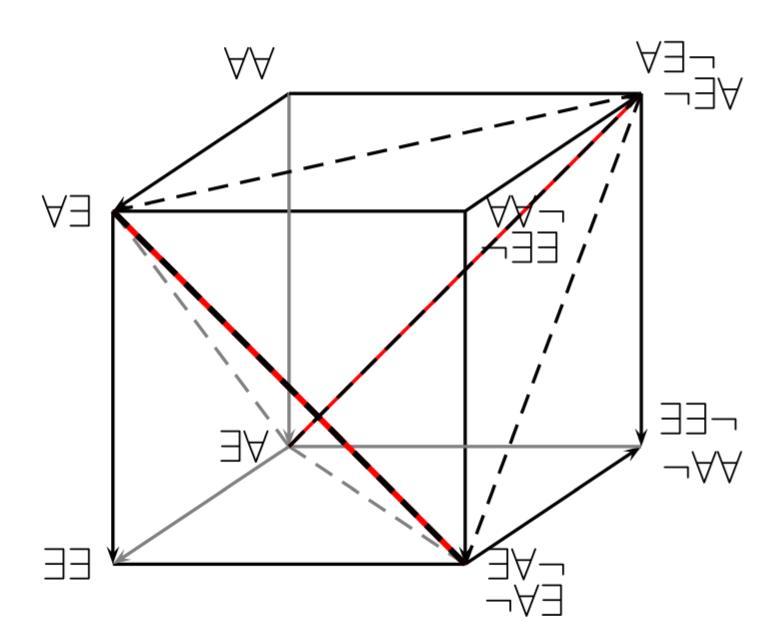
A Cube of Opposition for Predicate Logic (2020), p. 109
by Nilsson, Jørgen Fischer
Copyright according to our policy
Caption
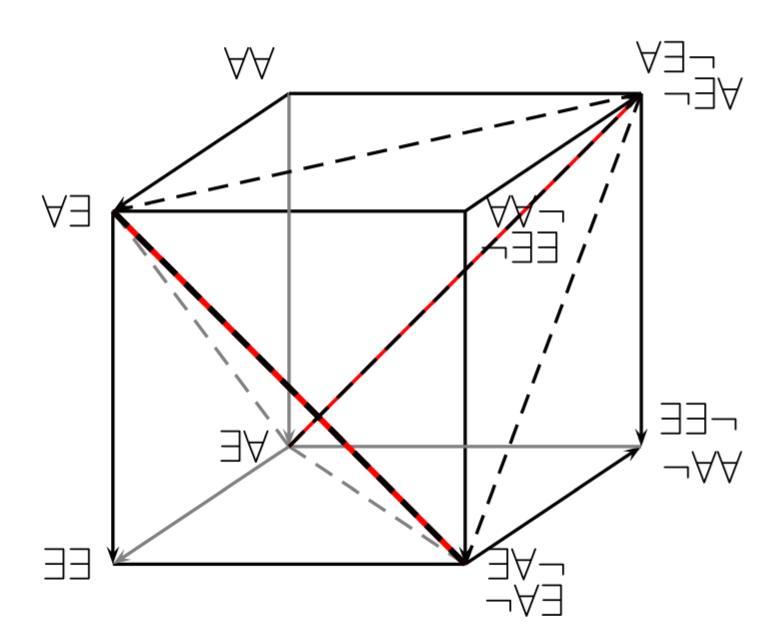
- Cube with embedded tetrahedron for disparatae
- Aristotelian family
- Buridan Sigma-4
- Boolean complexity
- 6
- Number of labels per vertex (at most)
- 2
- Equivalence between (some) labels of the same vertex
- Yes
- Analogy between (some) labels of the same vertex
- No
- Errors in the diagram
- No
- Shape
- Cube (regular)
- Colinearity range
- 0
- Coplanarity range
- 0
- Cospatiality range
- 0
- Representation of contradiction
- By some other geometric feature
Logic
Geometry
- Conceptual info
- No
- Mnemonic support (AEIO, purpurea ...)
- No
- Form
- none
- Label type
- symbolic
- Symbolic field
- logic
- Contains partial formulas or symbols
- Yes
- Logical system
- predicate logic
Vertex description
Edge description
- Diagram is colored
- Yes
- Diagram is embellished
- No
- Tags
- composed operator duality
Style
Additional notes
- Let $C,D$ be unary predicates and $R$ a binary relation.
$\forall\forall$ stands for $\forall x( Cx \to \forall y (Dy \to Rxy)$
$\forall\exists$ stands for $\forall x( Cx \to \exists y (Dy \wedge Rxy)$
$\exists\forall$ stands for $\exists x( Cx \wedge \forall y (Dy \to Rxy)$
$\exists\exists$ stands for $\exists x( Cx \wedge \exists y (Dy \wedge Rxy)$
$\forall\forall\neg$ stands for $\forall x( Cx \to \forall y (Dy \to \neg Rxy)$
$\neg\exists\exists$ stands for $\neg\exists x( Cx \wedge \exists y (Dy \wedge Rxy)$
$\forall\exists\neg$ stands for $\forall x( Cx \to \exists y (Dy \wedge \neg Rxy)$
$\neg\exists\forall$ stands for $\neg\exists x( Cx \wedge \forall y (Dy \to Rxy)$
$\exists\forall\neg$ stands for $\exists x( Cx \wedge \forall y (Dy \to\neg Rxy)$
$\neg\forall\exists$ stands for $\neg\forall x( Cx \to \exists y (Dy \wedge Rxy)$
$\exists\exists\neg$ stands for $\exists x( Cx \wedge \exists y (Dy \wedge\neg Rxy)$
$\neg\forall\forall$ stands for $\neg\forall x( Cx \to \forall y (Dy \to Rxy)$
(Cf. pp. 104-105.)