A Cube of Opposition for Predicate Logic (2020), p. 108
by Nilsson, Jørgen Fischer
Copyright according to our policy
Caption
- The cube clad for Aristotelian modal logic
- Aristotelian family
- Buridan Sigma-4
- Boolean complexity
- 6
- Number of labels per vertex (at most)
- 2
- Equivalence between (some) labels of the same vertex
- Yes
- Analogy between (some) labels of the same vertex
- No
- Uniqueness of the vertices up to logical equivalence
- Yes
- Errors in the diagram
- No
- Shape
- Cube (regular)
- Colinearity range
- 0
- Coplanarity range
- 0
- Cospatiality range
- 0
- Representation of contradiction
- By some other geometric feature
Logic
Geometry
- Conceptual info
- No
- Mnemonic support (AEIO, purpurea ...)
- No
- Form
- none
- Label type
- symbolic
- Symbolic field
- logic
- Contains partial formulas or symbols
- Yes
- Logical system
- modal syllogistics
Vertex description
Edge description
- Diagram is colored
- No
- Diagram is embellished
- No
- Tags
- composed operator duality
Style
Additional notes
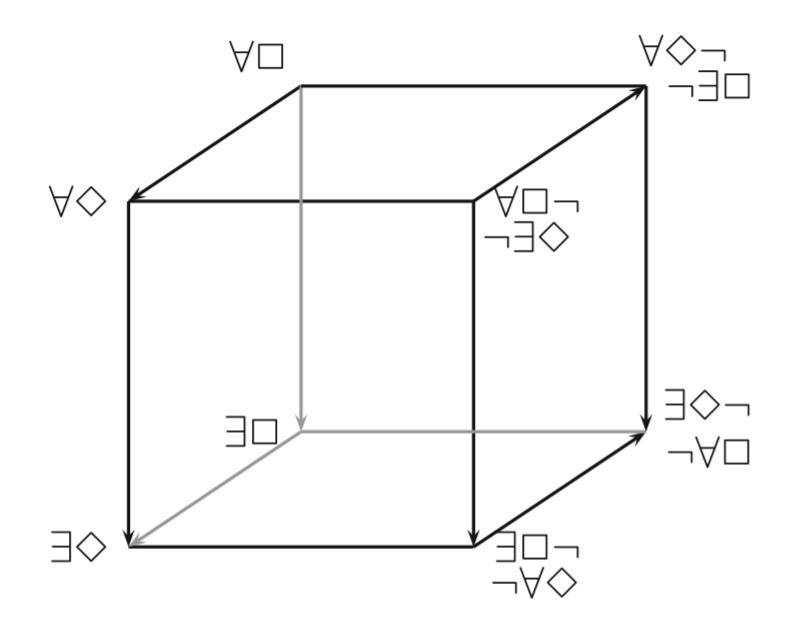
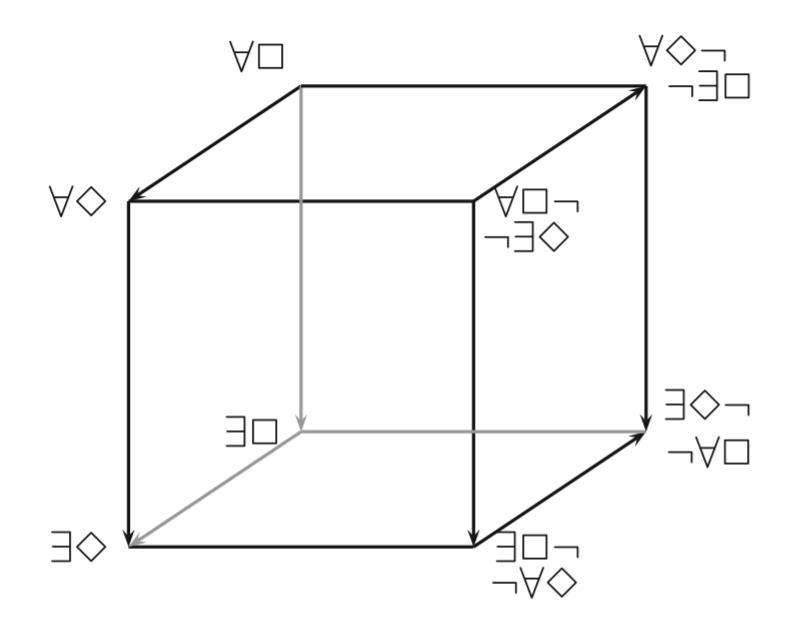
- Let $C,D$ be unary predicates.
$\forall\Box$ stands for $\forall x( Cx \to \Box Dx)$
$\forall\Diamond$ stands for $\forall x( Cx \to \Diamond Dx)$
$\exists\Box$ stands for $\exists x( Cx \wedge \Box Dx)$
$\exists\Diamond$ stands for $\exists x( Cx \wedge \Diamond Dx)$
$\forall\Box\neg$ stands for $\forall x( Cx \to \Box \neg Dx)$
$\neg\exists\Diamond$ stands for $\neg\exists x( Cx \wedge \Diamond Dx)$
$\forall\Diamond\neg$ stands for $\forall x( Cx \to \Diamond \neg Dx)$
$\neg\exists\Box$ stands for $\neg\exists x( Cx \wedge \Box Dx)$
$\exists\Box\neg$ stands for $\exists x( Cx \wedge \Box\neg Dx)$
$\neg\forall\Diamond$ stands for $\neg\forall x( Cx \to \Diamond Dx)$
$\exists\Diamond\neg$ stands for $\exists x( Cx \wedge \Diamond\neg Dx)$
$\neg\forall\Box$ stands for $\neg\forall x( Cx \to \Box Dx)$
(Based on pp. 104-105.)
Note that Nilsson remains silent on the issue of ampliation, which would involve replacing all occurrences of $Cx$ with $\Diamond Cx$ in the formulas above.