A Cube of Opposition for Predicate Logic (2020), p. 107
by Nilsson, Jørgen Fischer
Copyright according to our policy
Caption
- Cube of opposition with R being equality
- Aristotelian family
- Buridan Sigma-4
- Boolean complexity
- 5
- Number of labels per vertex (at most)
- 2
- Equivalence between (some) labels of the same vertex
- Yes
- Analogy between (some) labels of the same vertex
- No
- Uniqueness of the vertices up to logical equivalence
- Yes
- Errors in the diagram
- No
- Shape
- Cube (regular)
- Colinearity range
- 0
- Coplanarity range
- 0
- Cospatiality range
- 0
- Representation of contradiction
- By some other geometric feature
Logic
Geometry
- Conceptual info
- No
- Mnemonic support (AEIO, purpurea ...)
- No
- Form
- none
- Label type
- linguistic
- Language
- English
- Lexical field
- unusual construction
- Contains partial sentences or single words
- No
- Contains abbreviations
- Yes
Vertex description
Edge description
- Diagram is colored
- No
- Diagram is embellished
- No
- Tags
- composed operator duality
Style
Additional notes
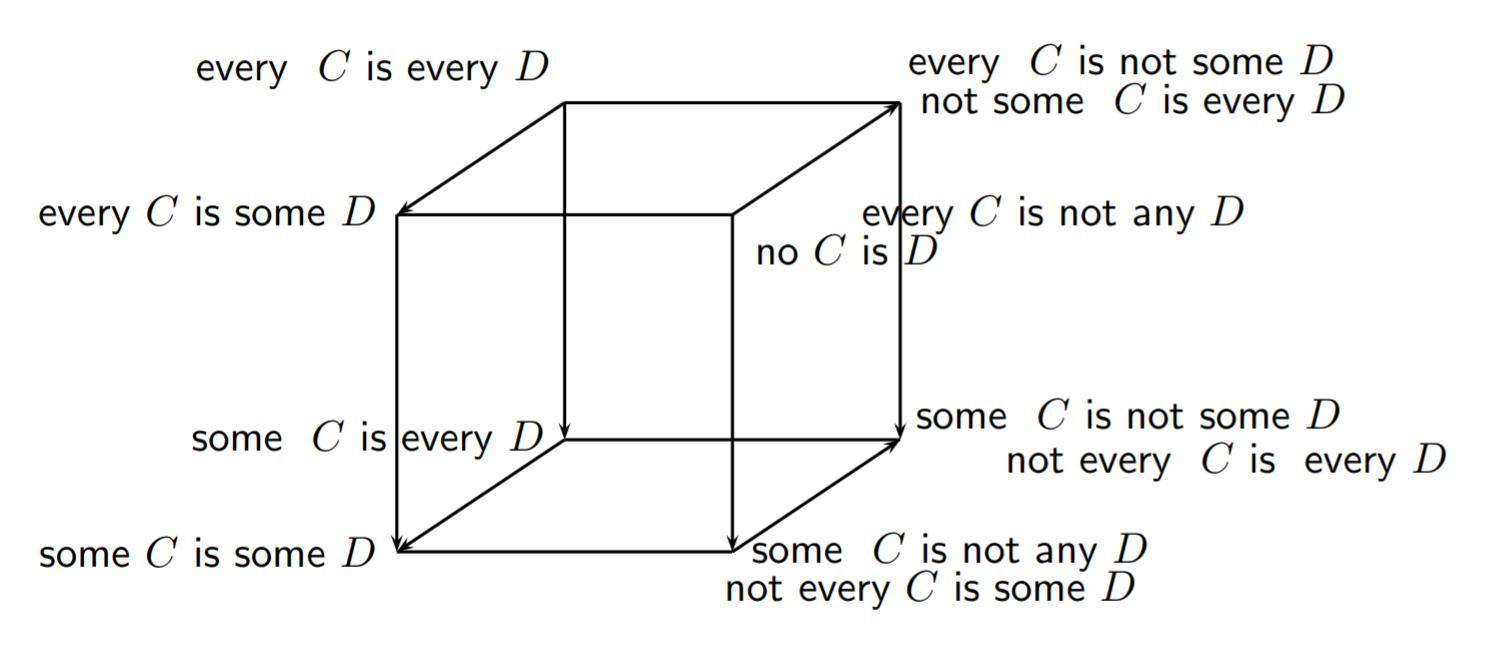
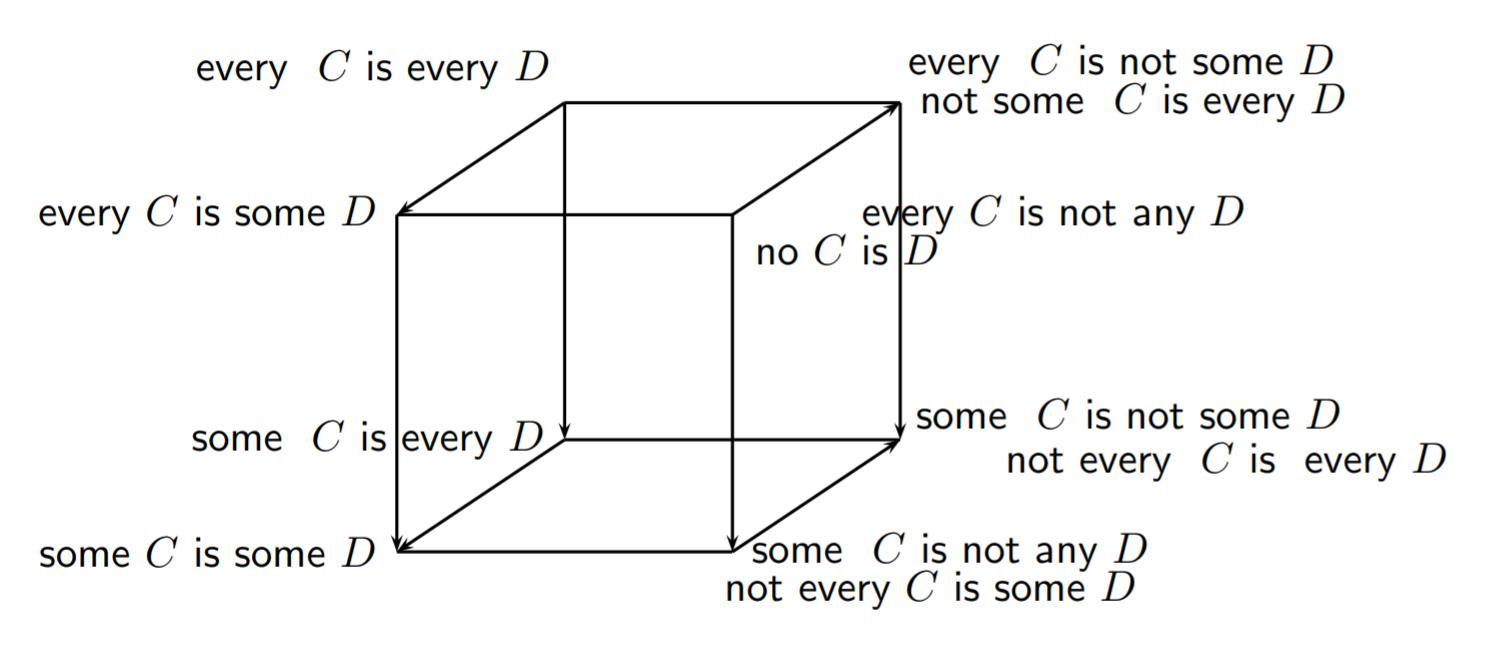
- Let $C,D$ be unary predicates and $R$ a binary relation.
$\forall\forall$ stands for $\forall x( Cx \to \forall y (Dy \to Rxy)$
$\forall\exists$ stands for $\forall x( Cx \to \exists y (Dy \wedge Rxy)$
$\exists\forall$ stands for $\exists x( Cx \wedge \forall y (Dy \to Rxy)$
$\exists\exists$ stands for $\exists x( Cx \wedge \exists y (Dy \wedge Rxy)$
$\forall\forall\neg$ stands for $\forall x( Cx \to \forall y (Dy \to \neg Rxy)$
$\neg\exists\exists$ stands for $\neg\exists x( Cx \wedge \exists y (Dy \wedge Rxy)$
$\forall\exists\neg$ stands for $\forall x( Cx \to \exists y (Dy \wedge \neg Rxy)$
$\neg\exists\forall$ stands for $\neg\exists x( Cx \wedge \forall y (Dy \to Rxy)$
$\exists\forall\neg$ stands for $\exists x( Cx \wedge \forall y (Dy \to\neg Rxy)$
$\neg\forall\exists$ stands for $\neg\forall x( Cx \to \exists y (Dy \wedge Rxy)$
$\exists\exists\neg$ stands for $\exists x( Cx \wedge \exists y (Dy \wedge\neg Rxy)$
$\neg\forall\forall$ stands for $\neg\forall x( Cx \to \forall y (Dy \to Rxy)$
(Cf. pp. 104-105.)
Note that interpreting R as identity does not change the Aristotelian family of the diagram (it remains a Buridan sigma-4), but it does imply that the Boolean complexity of this diagram goes down from 6 to 5. Cf. Lorenz Demey, 2019, Boolean considerations on John Buridan's octagons of opposition, History and Philosophy of Logic, 40: 116-134 (link).