Was Lewis Carroll an Amazing Oppositional Geometer? (2014), p. 402
by Moretti, Alessio
Copyright according to our policy
Caption
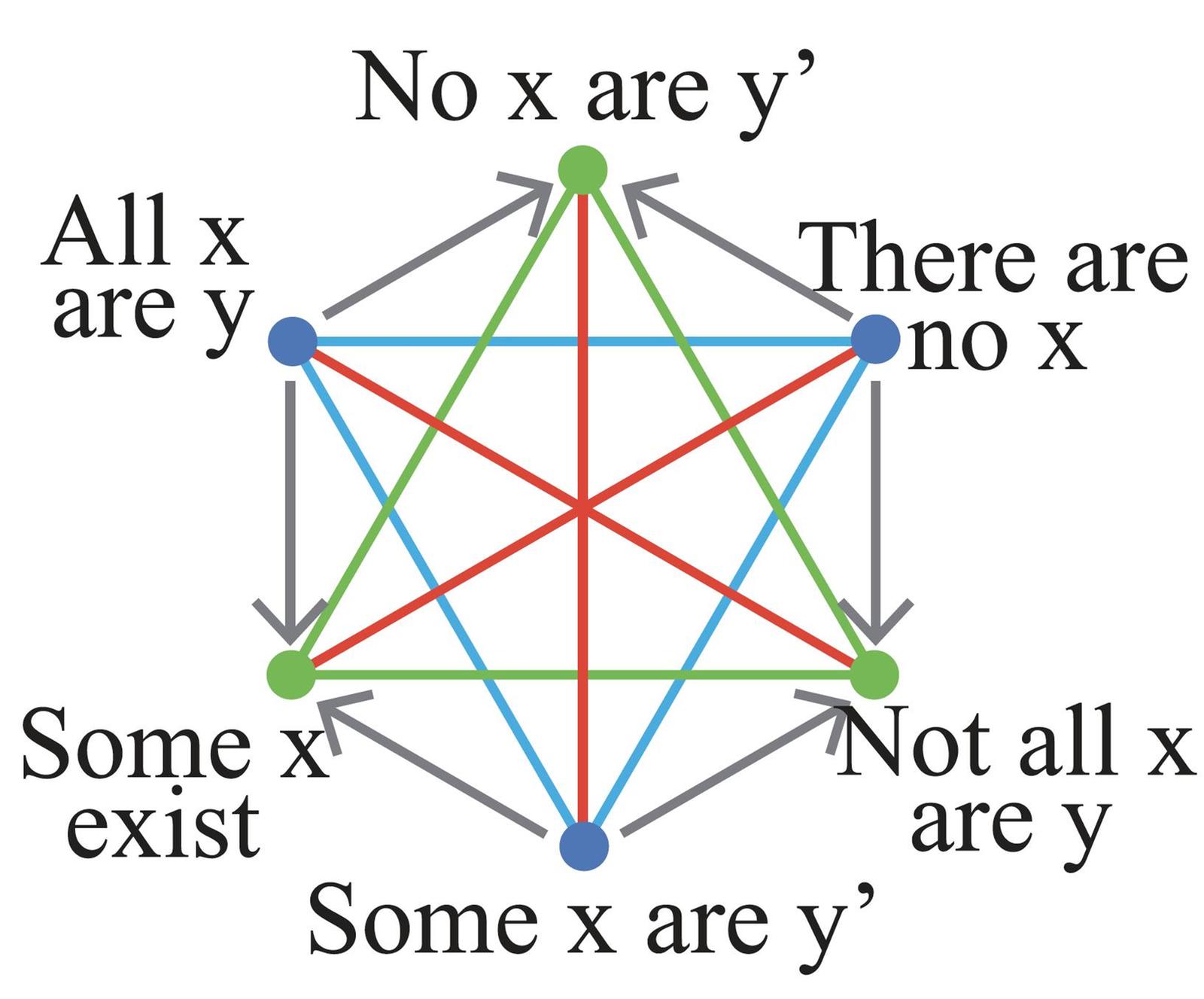
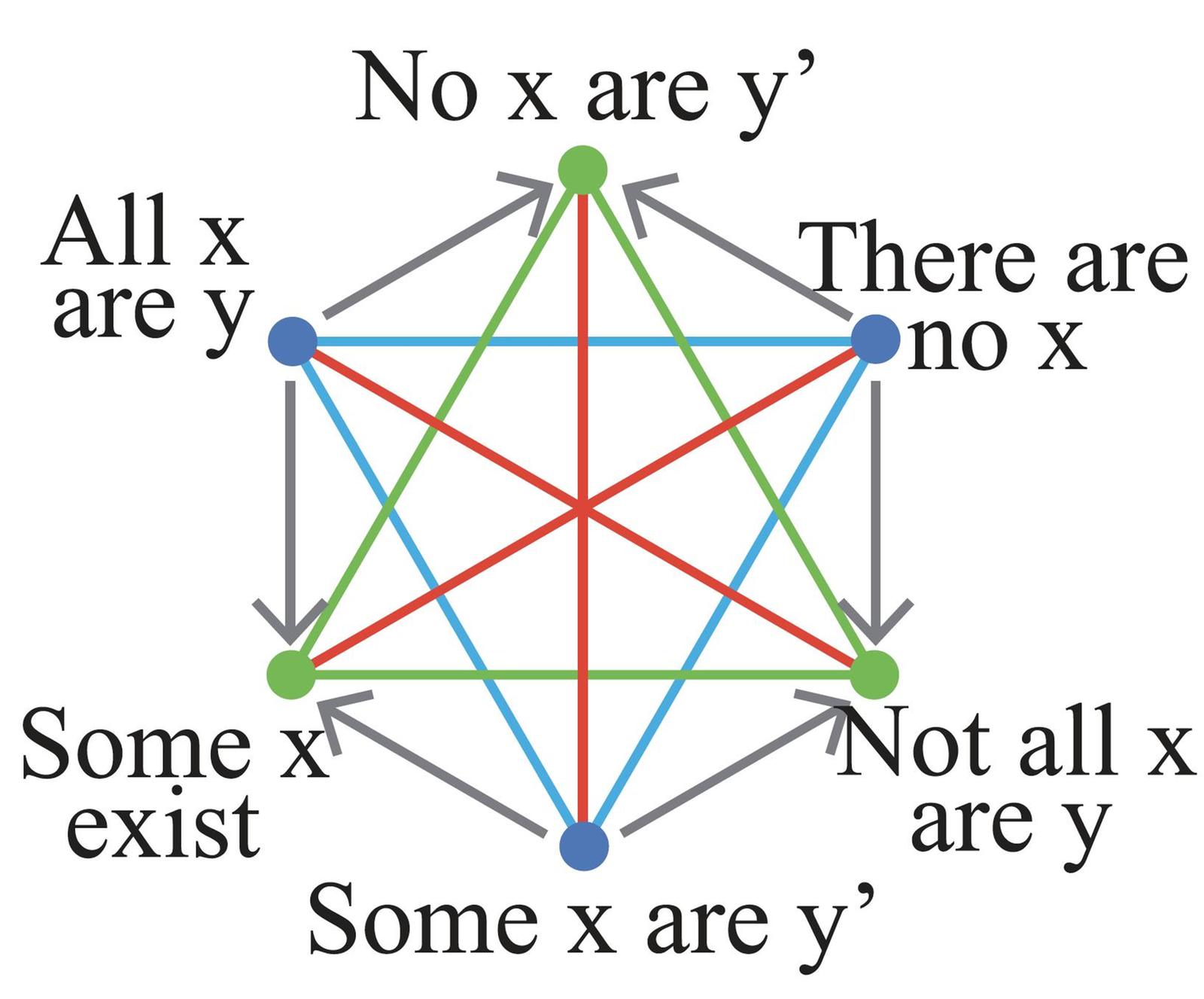
- Six Carrollian strong oppositional hexagons (indicial and vernacular reading).
- Aristotelian family
- Jacoby-Sesmat-Blanché Sigma-3
- Boolean complexity
- 3
- Number of labels per vertex (at most)
- 1
- Uniqueness of the vertices up to logical equivalence
- Yes
- Errors in the diagram
- No
- Shape
- Hexagon (regular)
- Colinearity range
- 0
- Coplanarity range
- 0
- Cospatiality range
- 0
- Representation of contradiction
- By central symmetry
Logic
Geometry
- Conceptual info
- No
- Mnemonic support (AEIO, purpurea ...)
- No
- Form
- dots
- Label type
- linguistic
- Language
- English
- Lexical field
- syllogistics
- Contains partial sentences or single words
- No
- Contains abbreviations
- Yes
Vertex description
Edge description
- Diagram is colored
- Yes
- Diagram is embellished
- No
- Tags
- Boolean closed ;
- existential import
Style
Additional notes
- Consider the following partition:
1) A! (all x are y, and there is at least one x)
2) I $\wedge$ O (some x are y and some x are not y)
3) E! (no x are y, and there is at least one x)
4) there are no x
With the bitstrings based on this partition, the formulas of this diagram (in vernacular notation) can be represented as follows:
1000 = all x are y
0100 = some x are y and some x are y'
0010 = all x are y'
0001 = there are no x
1100 = some x are y
1010 = all x are y or all [x] are y'
1001 = no x are y'
0110 = some x are y'
0101 = not all x are y nor are all y' [not all x are y and not all x are y']
0011 = no x are y
1110 = some x exist
1101 = not all x are y'
1011 = no x are y or none [i.e. no x] are y'
0111 = not all x are y