Was Lewis Carroll an Amazing Oppositional Geometer? (2014), p. 394
by Moretti, Alessio
Copyright according to our policy
Caption
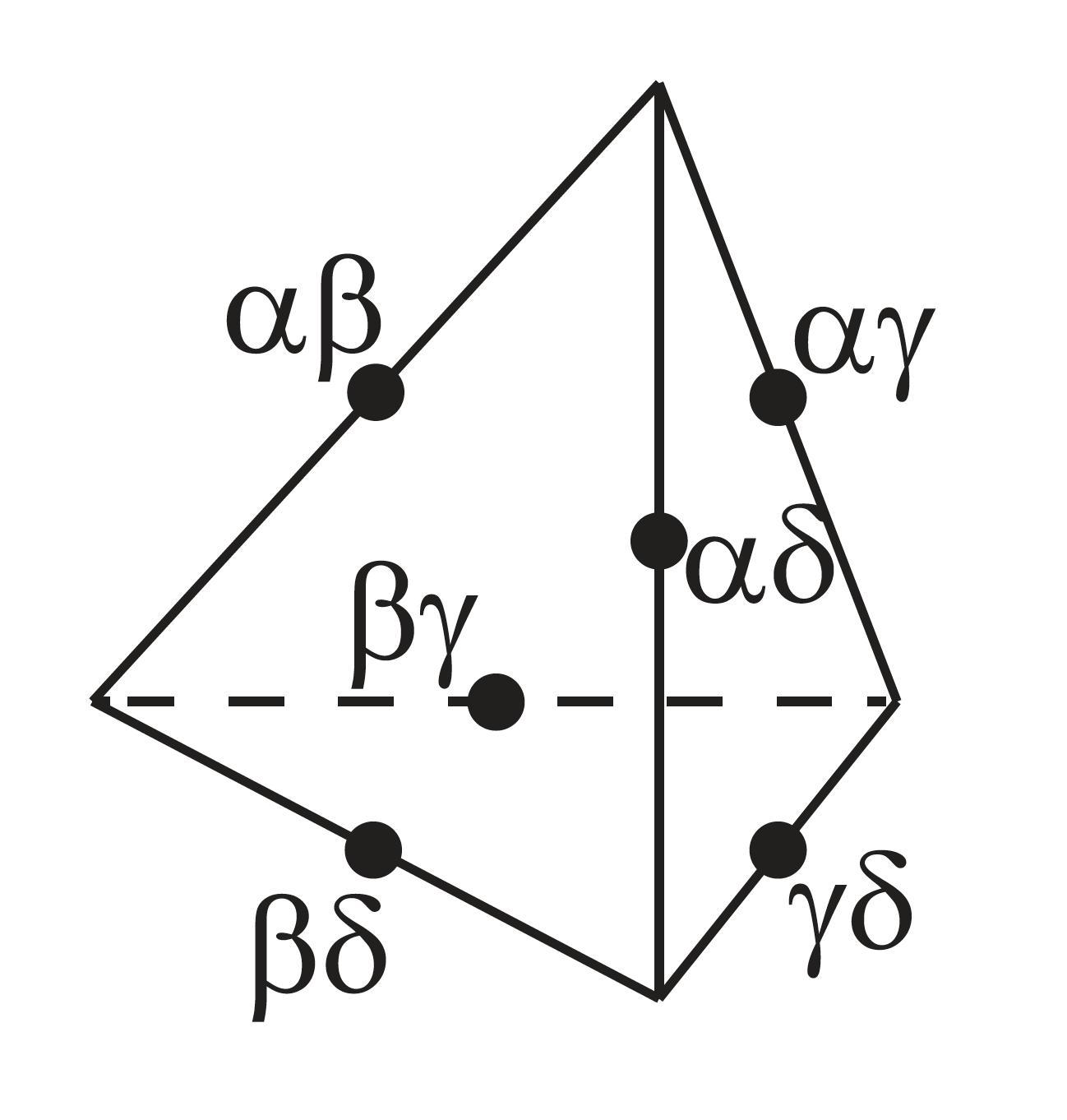
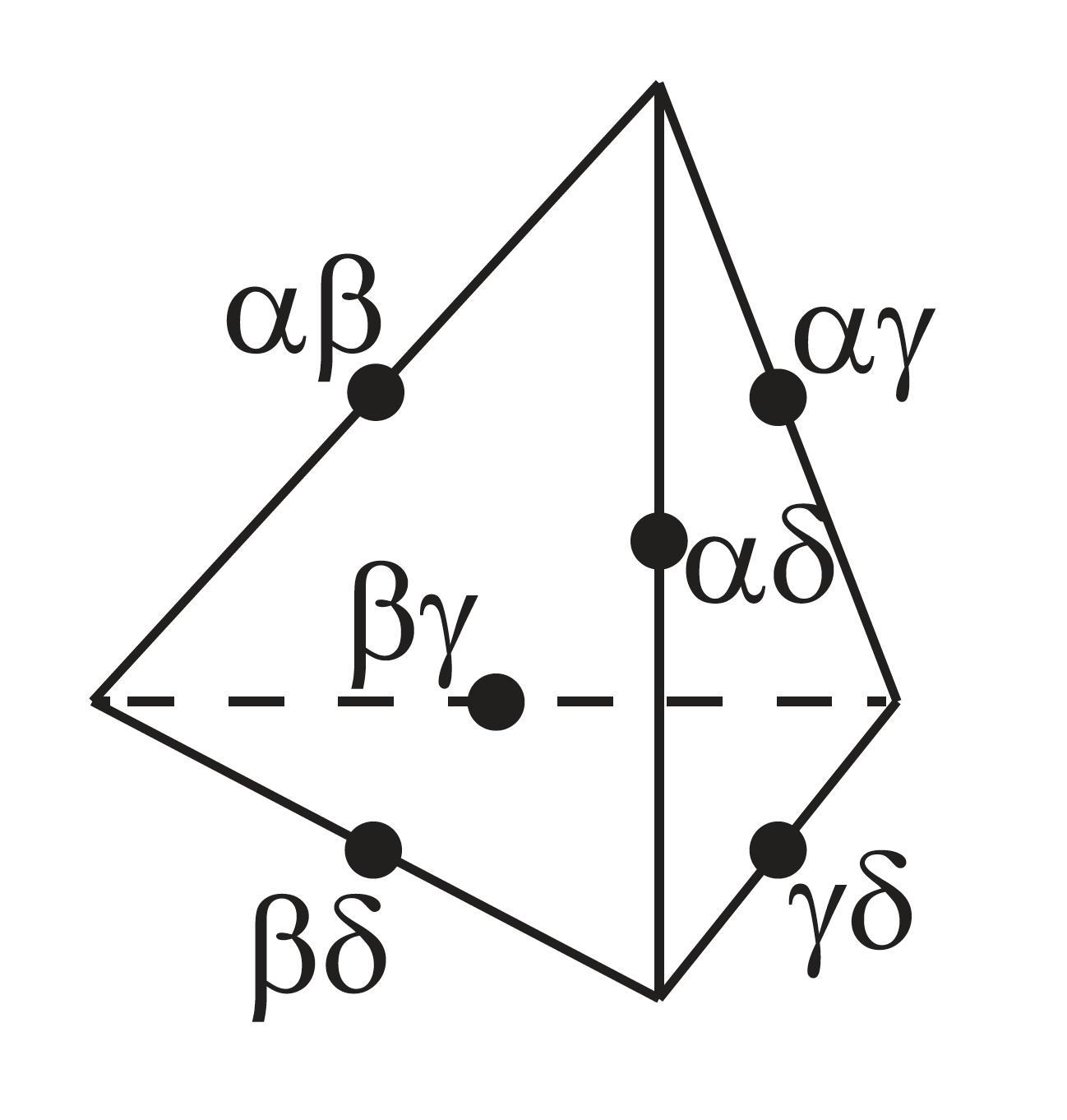
- Each of the six vertices lying in the middle of one of the edges has its contradictory negation in the vertex lying in the middle of the edge opposed to it.
- Aristotelian family
- Degenerate Sigma-3 with Unconnectedness 12
- Boolean complexity
- 4
- Number of labels per vertex (at most)
- 1
- Uniqueness of the vertices up to logical equivalence
- Yes
- Errors in the diagram
- No
- Shape
- Octahedron (regular)
- Colinearity range
- 0
- Coplanarity range
- 0
- Cospatiality range
- 0
- Representation of contradiction
- By central symmetry
Logic
Geometry
- Conceptual info
- No
- Mnemonic support (AEIO, purpurea ...)
- No
- Form
- dots
- Label type
- symbolic
- Symbolic field
- logic
- Contains partial formulas or symbols
- Yes
- Logical system
- predicate logic
Vertex description
Edge description
- Diagram is colored
- No
- Diagram is embellished
- No
- Tags
- subdiagram ;
- existential import
Style
Additional notes
- Consider the following partition:
1) A! (all x are y, and there is at least one x)
2) I $\wedge$ O (some x are y and some x are not y)
3) E! (no x are y, and there is at least one x)
4) there are no x
With the bitstrings based on this partition, the formulas of this diagram (in Greek notation) can be represented as follows:
1000 = $ \alpha\beta\delta $
0100 = $ \alpha\beta\gamma $
0010 = $ \alpha\gamma\delta $
0001 = $ \beta\gamma\delta $
1100 = $ \alpha\beta $
1010 = $ \alpha\delta$
1001 = $ \beta\delta $
0110 = $ \alpha\gamma $
0101 = $ \beta\gamma $
0011 = $ \gamma\delta $
1110 = $ \alpha $
1101 = $ \beta $
1011 = $ \delta $
0111 = $ \gamma $
Note: $\alpha\beta$ means $\alpha\wedge\beta$ (cf. p. 391).
Note: the octahedron shape is easiest to see if the encompassing tetrahedron is tilted so that it stands on one of its edges.