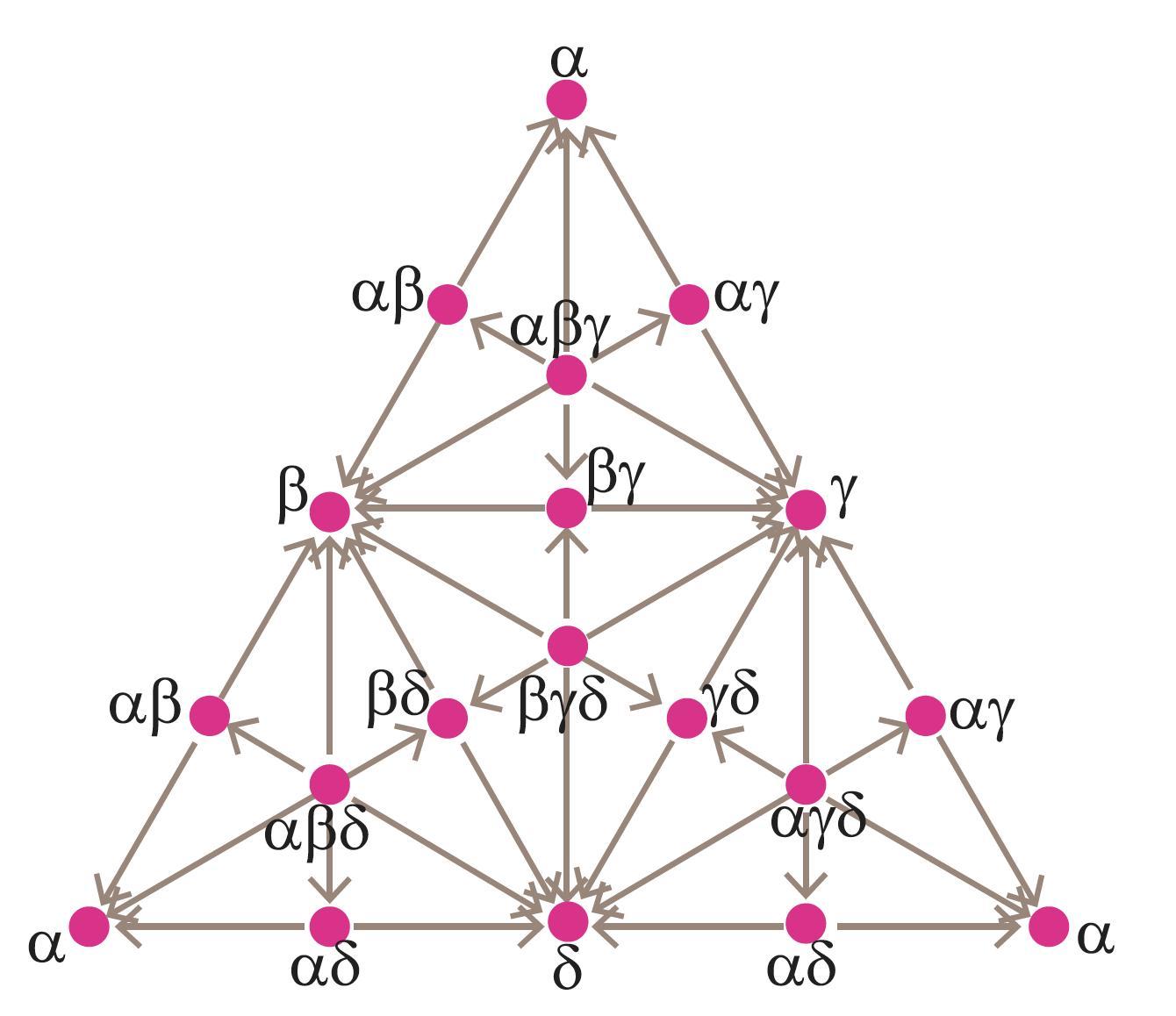
Was Lewis Carroll an Amazing Oppositional Geometer? (2014), p. 394
by Moretti, Alessio
Copyright according to our policy
Caption
- Arrows are more informative than lines (no harm being done to Carroll's logic).
- Aristotelian family
- Classical Sigma-7
- Boolean complexity
- 4
- Number of labels per vertex (at most)
- 1
- Uniqueness of the vertices up to logical equivalence
- No
- Errors in the diagram
- No
- Shape
- Triangle (regular)
- Colinearity range
- 0
- Coplanarity range
- 0
- Cospatiality range
- 0
- Representation of contradiction
- By some other geometric feature
Logic
Geometry
- Conceptual info
- No
- Mnemonic support (AEIO, purpurea ...)
- No
- Form
- dots
- Label type
- symbolic
- Symbolic field
- logic
- Contains partial formulas or symbols
- Yes
- Logical system
- predicate logic
Vertex description
Edge description
- Diagram is colored
- Yes
- Diagram is embellished
- No
- Tags
- Boolean closed ;
- existential import
Style
Additional notes
- Consider the following partition:
1) A! (all x are y, and there is at least one x)
2) I $\wedge$ O (some x are y and some x are not y)
3) E! (no x are y, and there is at least one x)
4) there are no x
With the bitstrings based on this partition, the formulas of this diagram (in Greek notation) can be represented as follows:
1000 = $ \alpha\beta\delta $
0100 = $ \alpha\beta\gamma $
0010 = $ \alpha\gamma\delta $
0001 = $ \beta\gamma\delta $
1100 = $ \alpha\beta $
1010 = $ \alpha\delta$
1001 = $ \beta\delta $
0110 = $ \alpha\gamma $
0101 = $ \beta\gamma $
0011 = $ \gamma\delta $
1110 = $ \alpha $
1101 = $ \beta $
1011 = $ \delta $
0111 = $ \gamma $
Note: $\alpha\beta$ means $\alpha\wedge\beta$ (cf. p. 391).
Note that $\alpha$ occurs three times in this diagram (viz., on the three vertices of the large triangle), and that each of $\alpha\beta$, $\alpha\gamma$ and $\alpha\delta$ occurs two times in this diagram (viz., twice on each edge of the large triangle).