Why the Logical Hexagon? (2012), p. 84
by Moretti, Alessio

Copyright according to our policy
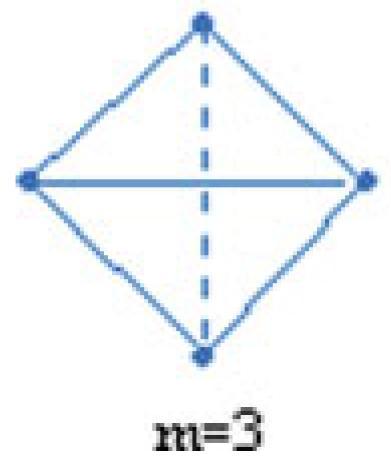
Caption
- $\textit{n}$-contrariety as simpliciality of dim. $\textit{m}$
- Aristotelian family
- Contrariety 4-clique
- Boolean complexity
- 4–5
- Number of labels per vertex (at most)
- 0
- Errors in the diagram
- No
- Shape
- Kite (irregular)
- Colinearity range
- 0
- Coplanarity range
- 0
- Cospatiality range
- 0
- Representation of contradiction
- N.A.
Logic
Geometry
- Conceptual info
- Yes
- Mnemonic support (AEIO, purpurea ...)
- No
- Form
- dots
- Label type
- none
- Contains definitions of relations
- No
- Form
- solid lines ,
- dashed lines
- Has arrowheads
- No
- Overlap
- No
- Curved
- No
- Hooked
- No
- As wide as vertices
- No
- Contains text
- No
- Label type
- none
Vertex description
Edge description
- Diagram is colored
- Yes
- Diagram is embellished
- No
Style
Additional notes
- The negation closure of this diagram is a Moretti-Pellissier sigma-4.