Kant's Antinomies of Pure Reason and the 'Hexagon of Predicate Negation' (2020), p. 61
by McLaughlin, Peter; Schlaudt, Oliver

Copyright according to our policy

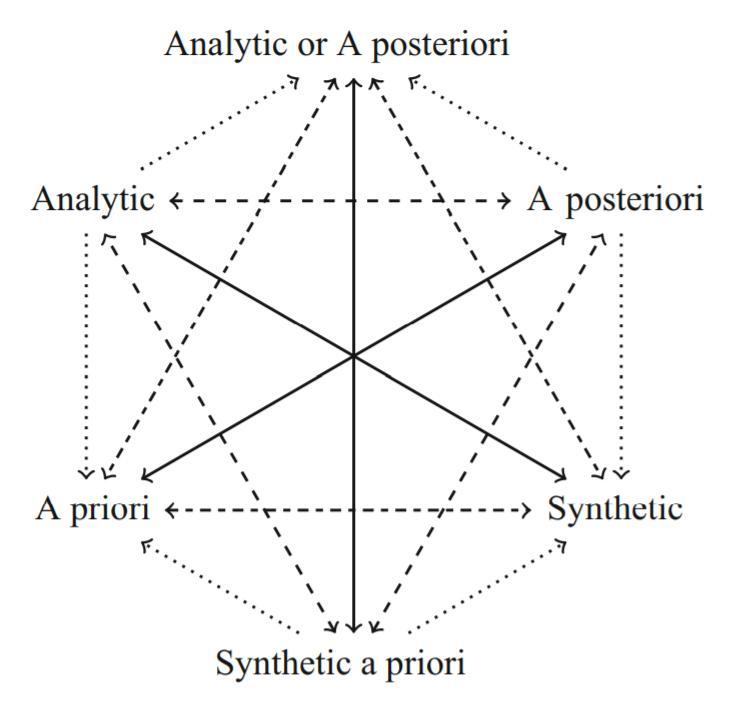
Caption

The “Kantian hexagon” from [4], 27

Logic

Aristotelian family

Jacoby-Sesmat-Blanché Sigma-3

Boolean complexity

3

Number of labels per vertex (at most)

1

Uniqueness of the vertices up to logical equivalence

Yes

Errors in the diagram

No

Geometry

Shape

Hexagon (regular)

Colinearity range

0

Coplanarity range

0

Cospatiality range

0

Representation of contradiction

By central symmetry

Graph structure

Synthetic a priori

• Contradiction with Analytic or A posteriori
• Contrariety with Analytic
• Contrariety with A posteriori
• Subalternation to Synthetic
• Subalternation to A priori

Analytic

• Contradiction with Synthetic
• Contrariety with Synthetic a priori
• Contrariety with A posteriori
• Subalternation to A priori
• Subalternation to Analytic or A posteriori

A priori

• Contradiction with A posteriori
• Subcontrariety with Synthetic
• Subcontrariety with Analytic or A posteriori
• Subalternation from Synthetic a priori
• Subalternation from Analytic

Analytic or A posteriori

• Contradiction with Synthetic a priori
• Subcontrariety with Synthetic
• Subcontrariety with A priori
• Subalternation from A posteriori
• Subalternation from Analytic

A posteriori

• Contradiction with A priori
• Contrariety with Analytic
• Contrariety with Synthetic a priori
• Subalternation to Analytic or A posteriori
• Subalternation to Synthetic

Synthetic

• Contradiction with Analytic
• Subcontrariety with Analytic or A posteriori
• Subcontrariety with A priori
• Subalternation from Synthetic a priori
• Subalternation from A posteriori

Vertex description

Conceptual info

No

Mnemonic support (AEIO, purpurea ...)

No

Form

none

Label type

linguistic

Language

English

Lexical field

philosophy

Contains partial sentences or single words

Yes

Contains abbreviations

No

Edge description

Style

Diagram is colored

No

Diagram is embellished

No

Tags

Boolean closed

;

Kant

Is a representation of

Beziau, Jean-Yves. 2012. “The Power of the Hexagon.” Logica Universalis 6 (1–2): 1–43. (p. 27)