Display Conventions for Octagons of Opposition (2024), p. 6
by Makinson, David

Copyright according to our policy
Caption
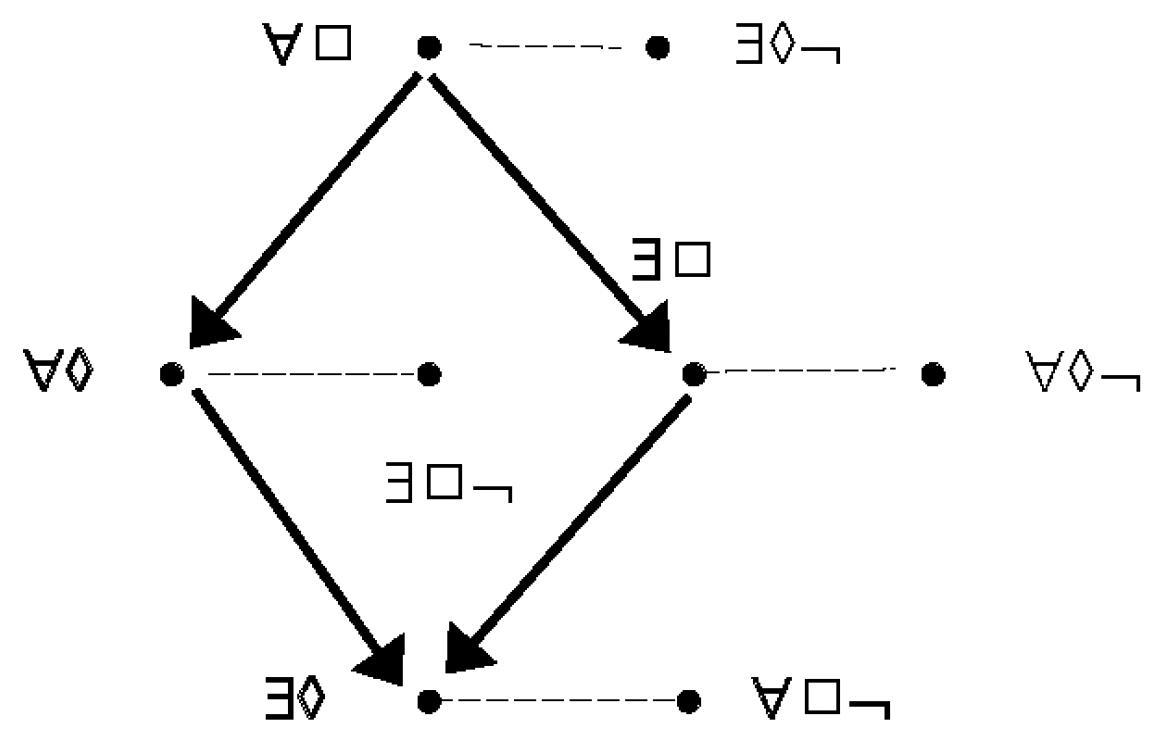
- Buridan’s modal octagon with all redundancies eliminated.
- Aristotelian family
- Buridan Sigma-4
- Boolean complexity
- 6
- Number of labels per vertex (at most)
- 1
- Uniqueness of the vertices up to logical equivalence
- Yes
- Errors in the diagram
- No
- Shape
- Hexagon (irregular)
- Colinearity range
- 0
- Coplanarity range
- 2
- Cospatiality range
- 0
- Representation of contradiction
- By some other geometric feature
Logic
Geometry
- Conceptual info
- No
- Mnemonic support (AEIO, purpurea ...)
- No
- Form
- dots
- Label type
- symbolic
- Symbolic field
- logic
- Contains partial formulas or symbols
- Yes
- Logical system
- modal syllogistics
- Contains definitions of relations
- No
- Form
- bold solid lines ,
- none ,
- dashed lines
- Has arrowheads
- Yes
- Overlap
- No
- Curved
- No
- Hooked
- No
- As wide as vertices
- No
- Contains text
- No
- Label type
- none
Vertex description
Edge description
- Diagram is colored
- No
- Diagram is embellished
- No
- Tags
- composed operator duality
Style
Additional notes
- $\forall\Box\textcolor{white}{\neg}$ = all S are necessarily P = $\exists x \Diamond Sx \wedge \forall x (\Diamond Sx \to \Box Px)$
$\forall\Diamond\textcolor{white}{\neg}$ = all S possibly P = $\exists x \Diamond Sx \wedge \forall x (\Diamond Sx \to \Diamond Px)$
$\exists\Box\textcolor{white}{\neg}$ = some S are necessarily P = $\exists x (\Diamond Sx \wedge \Box Px)$
$\exists\Diamond\textcolor{white}{\neg}$ = some S are possibly P = $\exists x (\Diamond Sx \wedge \Diamond Px)$
$\forall\Box\neg$ = all S are necessarily not P = $\forall x (\Diamond Sx \to \Box \neg Px)$
$\forall\Diamond\neg$ = all S are possibly not P = $\forall x (\Diamond Sx \to \Diamond\neg Px)$
$\exists\Box\neg$ = some S are necessarily not P = $\neg\exists x \Diamond Sx \vee\exists x (\Diamond Sx \wedge \Box\neg Px)$
$\exists\Diamond\neg$ = some S are possibly not P = $\neg\exists x \Diamond Sx \vee\exists x (\Diamond Sx \wedge \Diamond\neg Px)$
Cf. p. 118 of this paper.