Display Conventions for Octagons of Opposition (2024), p. 4
by Makinson, David

Copyright according to our policy

Caption

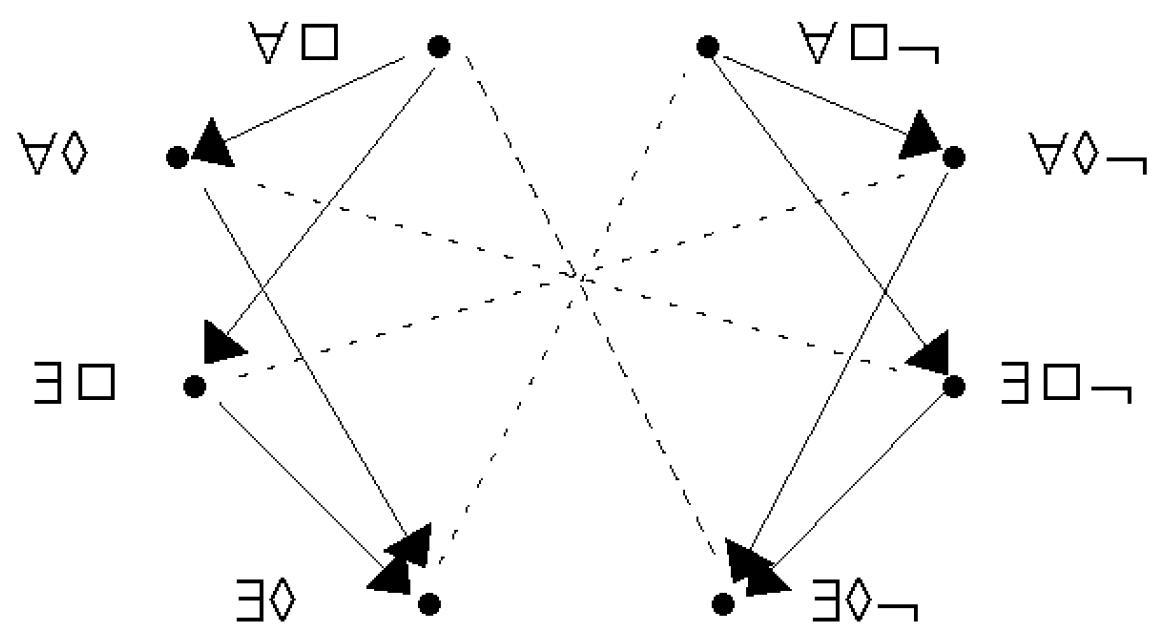
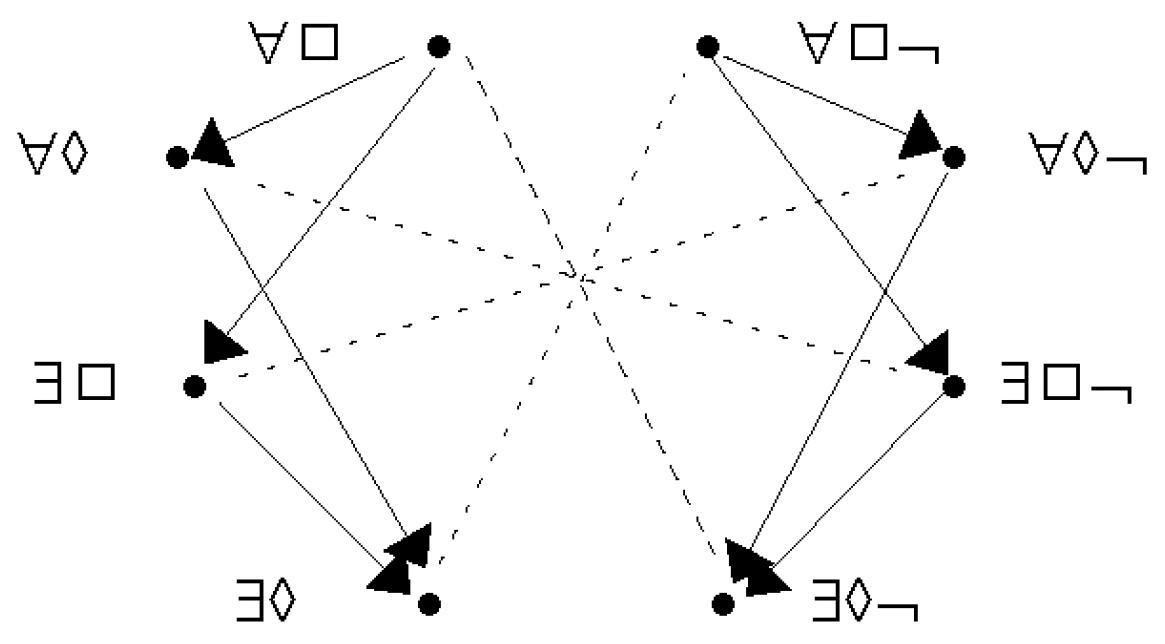
Buridan’s modal octagon pruned.

Logic

Aristotelian family

Buridan Sigma-4

Boolean complexity

6

Number of labels per vertex (at most)

1

Uniqueness of the vertices up to logical equivalence

Yes

Errors in the diagram

No

Geometry

Shape

Octagon (irregular)

Colinearity range

0

Coplanarity range

0

Cospatiality range

0

Representation of contradiction

By central symmetry

Vertex description

Conceptual info

No

Mnemonic support (AEIO, purpurea ...)

No

Form

dots

Label type

symbolic

Symbolic field

logic

Contains partial formulas or symbols

Yes

Logical system

modal syllogistics

Edge description

Contains definitions of relations

No

Form

solid lines

,

none

,

dashed lines

Has arrowheads

Yes

Overlap

No

Curved

No

Hooked

No

As wide as vertices

No

Contains text

No

Label type

none

Style

Diagram is colored

No

Diagram is embellished

No

Tags

composed operator duality

Additional notes

$\forall\Box\textcolor{white}{\neg}$ = all S are necessarily P = $\exists x \Diamond Sx \wedge \forall x (\Diamond Sx \to \Box Px)$
$\forall\Diamond\textcolor{white}{\neg}$ = all S possibly P = $\exists x \Diamond Sx \wedge \forall x (\Diamond Sx \to \Diamond Px)$
$\exists\Box\textcolor{white}{\neg}$ = some S are necessarily P = $\exists x (\Diamond Sx \wedge \Box Px)$
$\exists\Diamond\textcolor{white}{\neg}$ = some S are possibly P = $\exists x (\Diamond Sx \wedge \Diamond Px)$
$\forall\Box\neg$ = all S are necessarily not P = $\forall x (\Diamond Sx \to \Box \neg Px)$
$\forall\Diamond\neg$ = all S are possibly not P = $\forall x (\Diamond Sx \to \Diamond\neg Px)$
$\exists\Box\neg$ = some S are necessarily not P = $\neg\exists x \Diamond Sx \vee\exists x (\Diamond Sx \wedge \Box\neg Px)$
$\exists\Diamond\neg$ = some S are possibly not P = $\neg\exists x \Diamond Sx \vee\exists x (\Diamond Sx \wedge \Diamond\neg Px)$

Cf. p. 118 of this paper.