Theophrastische Modallogik (1969), p. 74
by Lorenzen, Paul
Copyright according to our policy
- Aristotelian family
- Non-Sigma
- Boolean complexity
- 4
- Number of labels per vertex (at most)
- 1
- Uniqueness of the vertices up to logical equivalence
- Yes
- Errors in the diagram
- No
- Shape
- Rectangle (irregular)
- Colinearity range
- 0–1
- Coplanarity range
- 3
- Cospatiality range
- 0
- Representation of contradiction
- N.A.
Logic
Geometry
- Conceptual info
- No
- Mnemonic support (AEIO, purpurea ...)
- No
- Form
- none
- Label type
- symbolic
- Symbolic field
- logic
- Contains partial formulas or symbols
- Yes
- Logical system
- modal logic
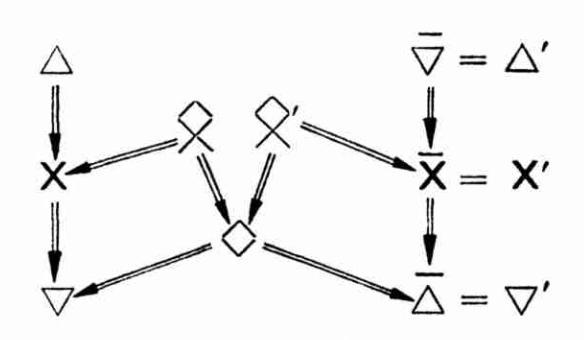
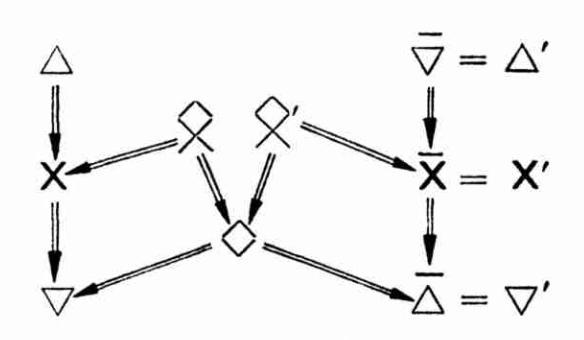
Vertex description
Edge description
- Diagram is colored
- No
- Diagram is embellished
- No
Style
Additional notes
- $\triangle p$ = it is necessary that $p$ (cf. p. 72).
$\triangledown p$ = it is possible that $p$ (cf. p. 73).
$\mathsf{X} p$ = it is true that $p$ (cf. p. 74).
$\hat{\times} p$ = $\mathsf{X}p \wedge \neg\triangle p$ (cf. p. 74).
$\diamond p$ = $\triangledown p \wedge \neg\triangle p$ (cf. p. 74).
The negation closure of this diagram is a sigma-6 diagram.