Symmetric Properties of the Syllogistic System Inherited from the Square of Opposition (2017), p. 97
by Kumova, Bora I.
Copyright according to our policy
Caption
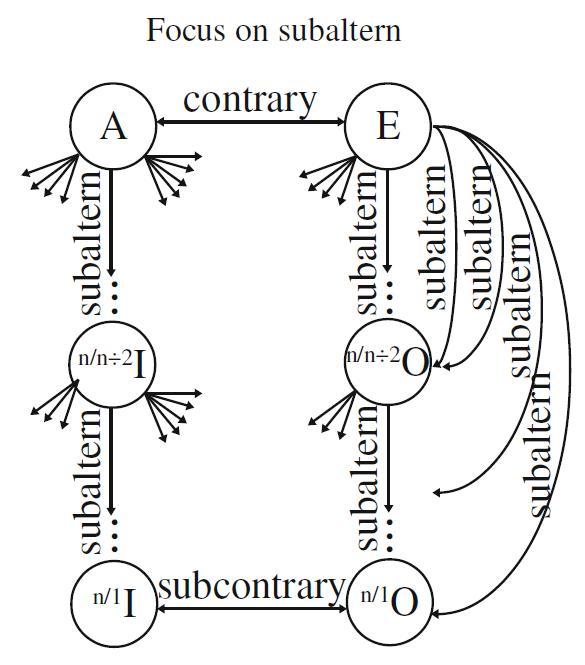
- n-quantified fuzzy-logical graph of opposition $^n\Omega$ with $n - 1$ fuzzy existential quantifiers and traditional relationships
- Aristotelian family
- Classical Sigma-2
- Boolean complexity
- 3
- Number of labels per vertex (at most)
- 1
- Uniqueness of the vertices up to logical equivalence
- No
- Errors in the diagram
- Yes
- Shape
- Rectangle (irregular)
- Colinearity range
- 0–1
- Coplanarity range
- 0
- Cospatiality range
- 0
- Representation of contradiction
- By central symmetry
Logic
Geometry
- Conceptual info
- No
- Mnemonic support (AEIO, purpurea ...)
- Yes
- Form
- circular
- Label type
- symbolic
- Symbolic field
- logic
- Contains partial formulas or symbols
- Yes
- Logical system
- syllogistics
- Contains definitions of relations
- No
- Form
- solid lines
- Has arrowheads
- Yes
- Overlap
- No
- Curved
- Yes
- Hooked
- No
- As wide as vertices
- No
- Contains text
- Yes
- Label type
- linguistic
- Language
- English
- Contains partial sentences or single words
- Yes
- Contain abbreviations
- No
Vertex description
Edge description
- Diagram is colored
- No
- Diagram is embellished
- No
Style
Additional notes
- Given that A is contradictory to all vertices on the right hand side (except for E), it follows that all these vertices on the right hand side (except for E) are logically equivalent to each other.
Given that E is contradictory to all vertices on the left hand side (except for A), it follows that all these vertices on the left hand side (except for A) are logically equivalent to each other.