
Logik im Recht. Grundlagen und Anwendungsbeispiele (2010), p. 310
by Joerden, Jan C.
Copyright according to our policy
Caption
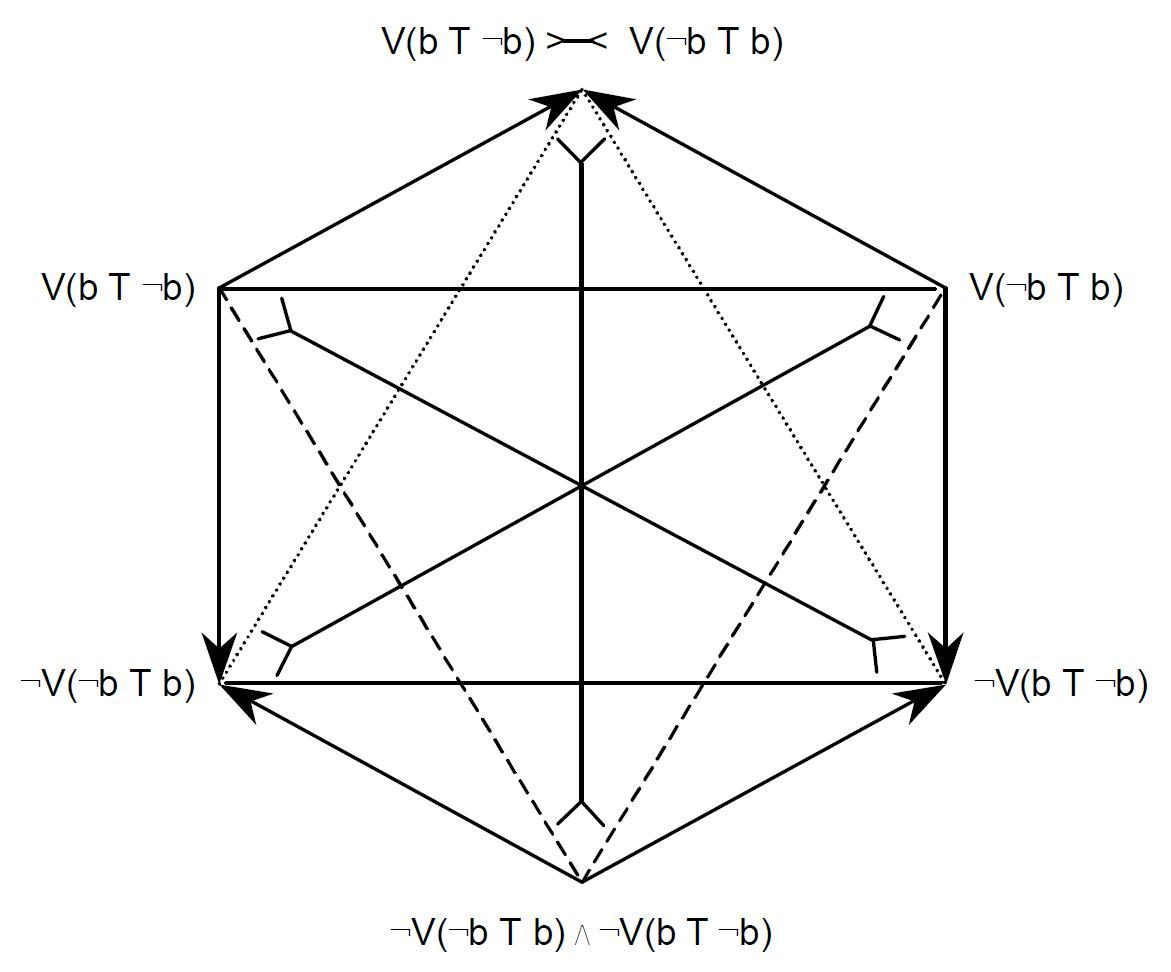
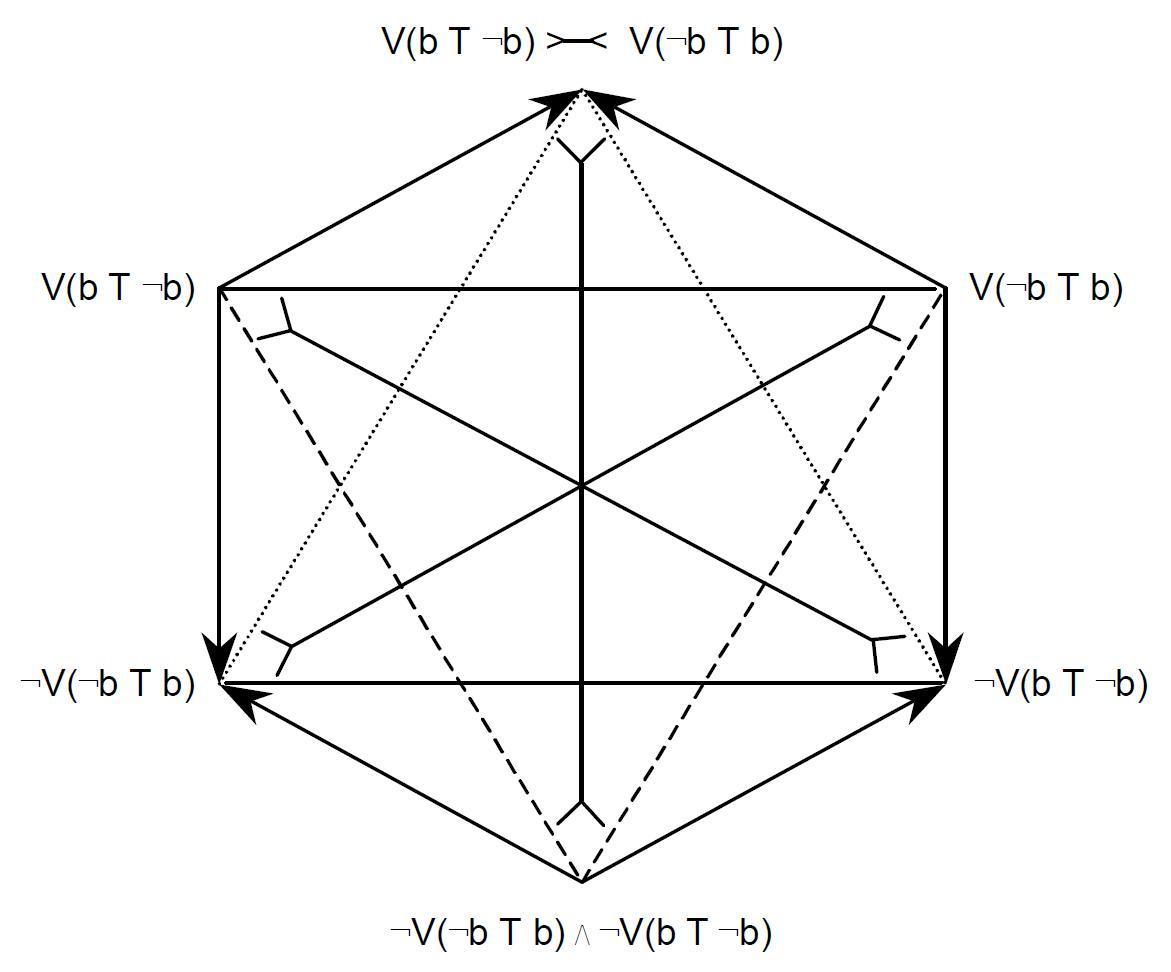
- Sechseck der Verbote und ihrer Negationen, die sich auf die Transformationen des Wechsels beziehen
Legend

- Aristotelian family
- Jacoby-Sesmat-Blanché Sigma-3
- Boolean complexity
- 3
- Number of labels per vertex (at most)
- 1
- Uniqueness of the vertices up to logical equivalence
- Yes
- Errors in the diagram
- Yes
- Shape
- Hexagon (regular)
- Colinearity range
- 0
- Coplanarity range
- 0
- Cospatiality range
- 0
- Representation of contradiction
- By central symmetry
Logic
Geometry
- Conceptual info
- No
- Mnemonic support (AEIO, purpurea ...)
- No
- Form
- none
- Label type
- symbolic
- Symbolic field
- logic
- Contains partial formulas or symbols
- No
- Logical system
- deontic logic
- Contains definitions of relations
- No
- Form
- dotted lines ,
- solid lines ,
- dashed lines
- Has arrowheads
- Yes
- Overlap
- No
- Curved
- No
- Hooked
- No
- As wide as vertices
- No
- Contains text
- No
- Label type
- none
Vertex description
Edge description
- Diagram is colored
- No
- Diagram is embellished
- No
- Tags
- Boolean closed
Style
Additional notes
- This diagram is currently inconsistent. The minimal way to repair it is as follows:
* given the subalternation from V(bT$\neg$b) to $\neg$V($\neg$bTb), it follows that there is a contrariety between V(bT$\neg$b) and V($\neg$bTb), so the upper horizontal line should be a dashed line to indicate this contrariety (rather than the current solid line)
* given the subalternation from V(bT$\neg$b) to $\neg$V($\neg$bTb), it follows that there is a subcontrariety between $\neg$V($\neg$bTb) and $\neg$V(bT$\neg$b), so the lower horizontal line should be a dotted line to indicate this subcontrariety (rather than the current solid line)
Under these modifications, the diagram is a Jacoby-Sesmat-Blanché sigma-3 of Boolean complexity 3, as indicated in the annotation.