
Logik im Recht. Grundlagen und Anwendungsbeispiele (2010), p. 211
by Joerden, Jan C.
Copyright according to our policy
Caption
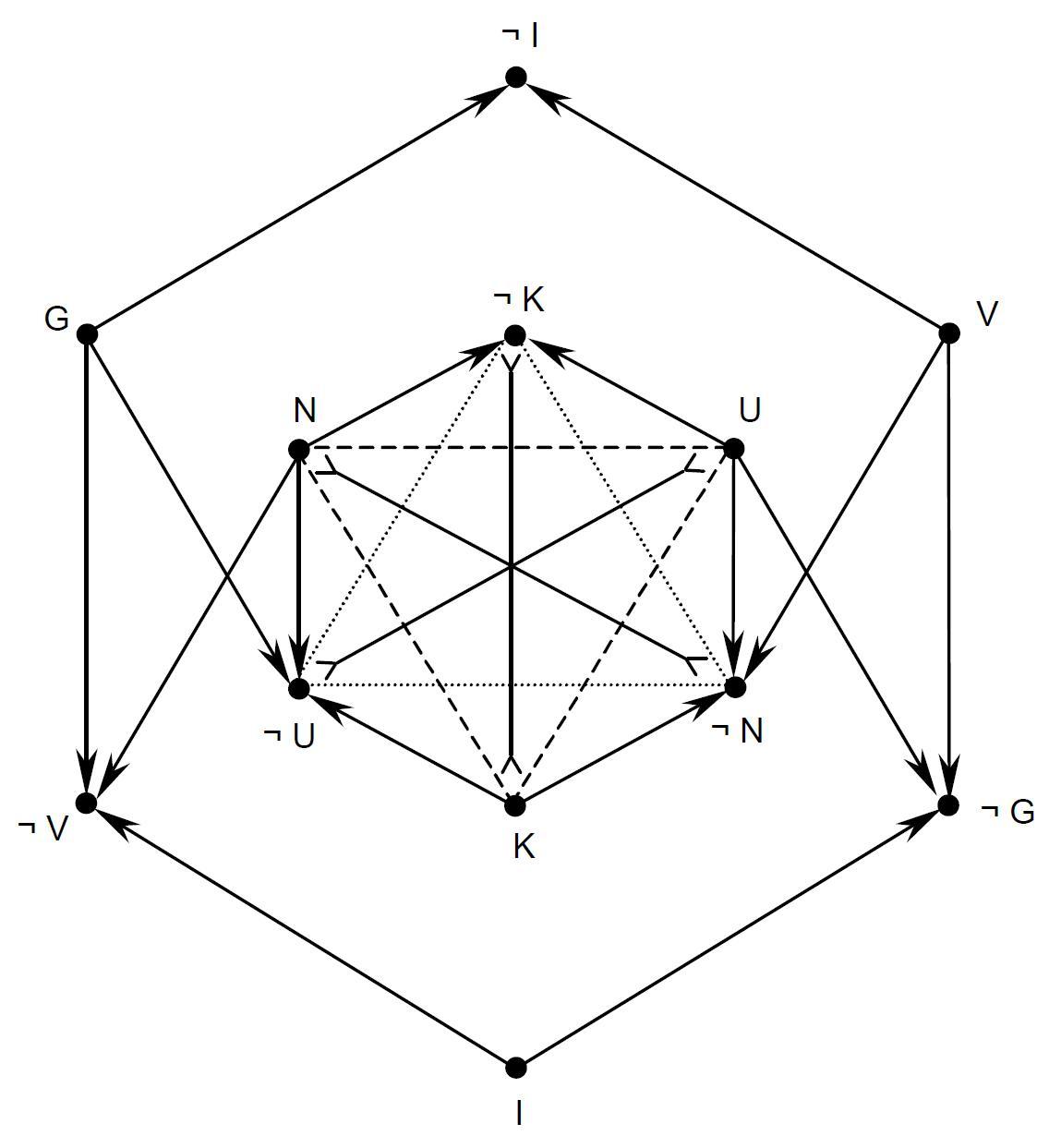
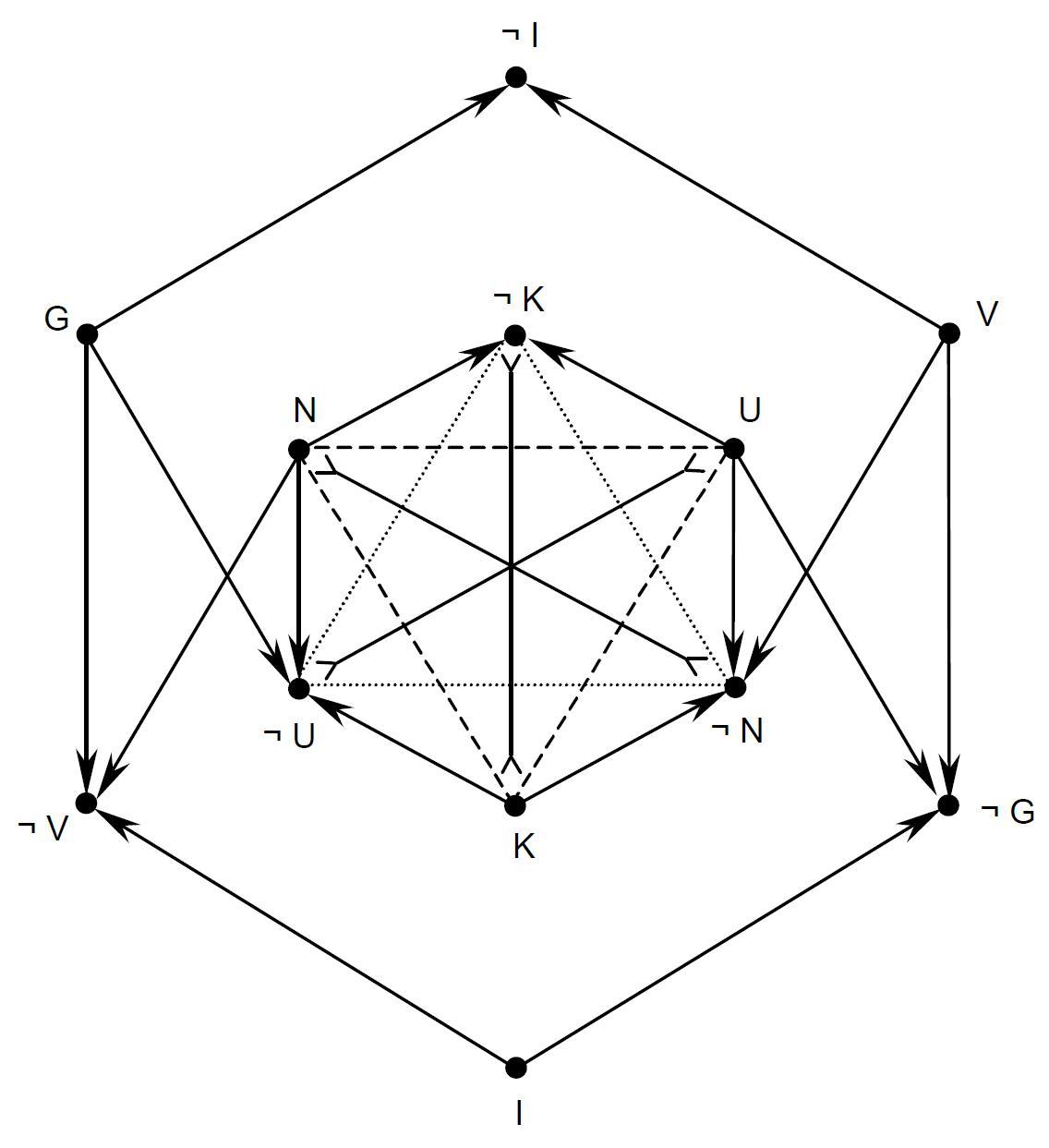
- Die Beziehungen zwischen Sollen und Sein (Ausgangsversion)
Legend

- Aristotelian family
- Sigma-6 Graph
- Boolean complexity
- 5
- Number of labels per vertex (at most)
- 1
- Uniqueness of the vertices up to logical equivalence
- Yes
- Errors in the diagram
- No
- Shape
- Hexagon (regular)
- Colinearity range
- 0
- Coplanarity range
- 6
- Cospatiality range
- 0
- Representation of contradiction
- By central symmetry
Logic
Geometry
- Conceptual info
- No
- Mnemonic support (AEIO, purpurea ...)
- No
- Form
- dots
- Label type
- symbolic
- Symbolic field
- logic
- Contains partial formulas or symbols
- Yes
- Logical system
- deontic logic ,
- modal logic
- Contains definitions of relations
- No
- Form
- dotted lines ,
- solid lines ,
- none ,
- dashed lines
- Has arrowheads
- Yes
- Overlap
- No
- Curved
- No
- Hooked
- No
- As wide as vertices
- No
- Contains text
- No
- Label type
- none
Vertex description
Edge description
- Diagram is colored
- No
- Diagram is embellished
- No
Style
Additional notes
- This diagram is still lacking some relations; the completed diagram can be found here.
The innermost hexagon consists of the alethic modalities; N = $\Box p$, U = $\Box\neg p$, K = $\Diamond p\wedge\Diamond\neg p$.
The outermost hexagon consists of the deontic modalities; G = $O p$, V = $O\neg p$, I = $P p\wedge P\neg p$.
This diagram induces the following 5-partition:
1) N ($\Box p$)
2) G $\wedge$ K = G $\wedge$ $\neg$N ($Op \wedge \Diamond\neg p$)
3) I ($Pp \wedge P\neg p$)
4) V $\wedge$ K = V $\wedge$ $\neg$U ($O\neg p \wedge \Diamond p$)
5) U ($\Box \neg p$)