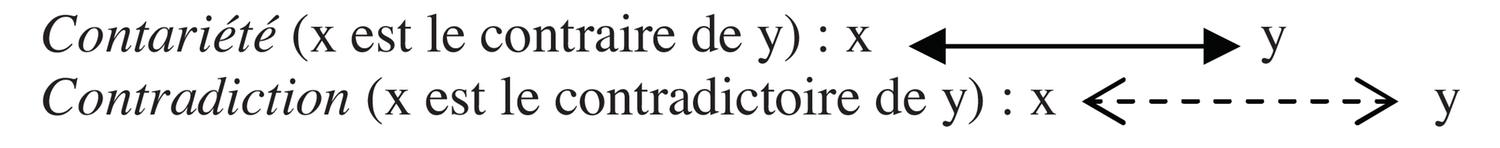
Les modalités en français. La validation des représentations (2010), p. 172
by Gosselin, Laurent
Copyright according to our policy
Caption
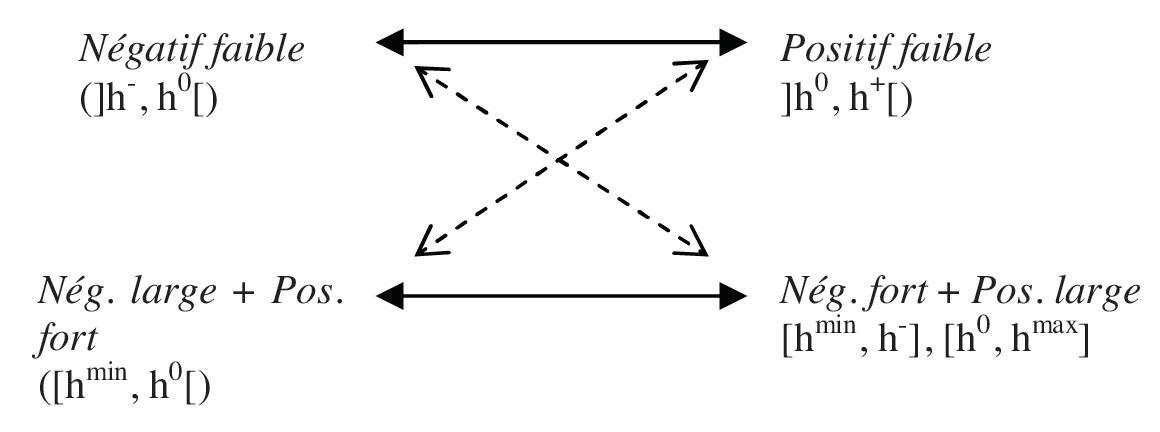
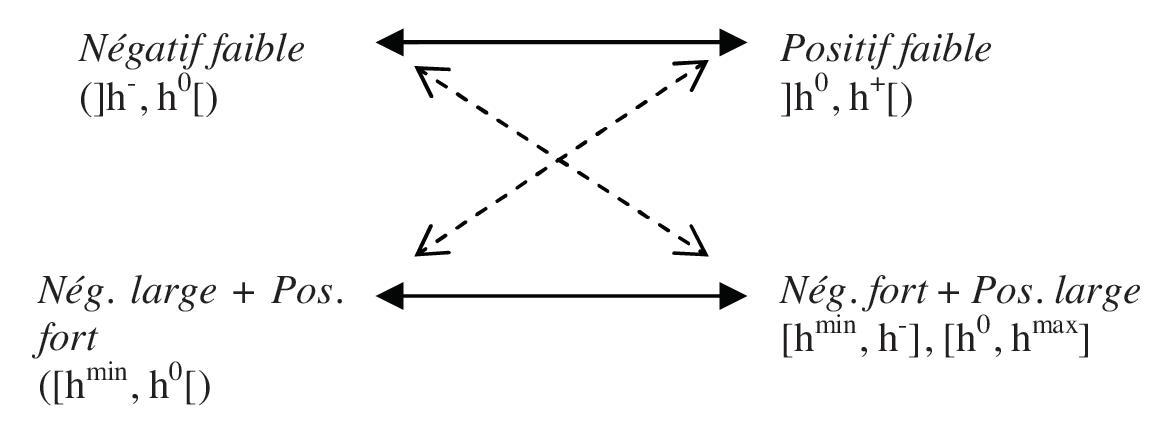
- Relations de contrariété (symétrie par rapport à h$^0$) et de contradiction (complémentarité)
Legend
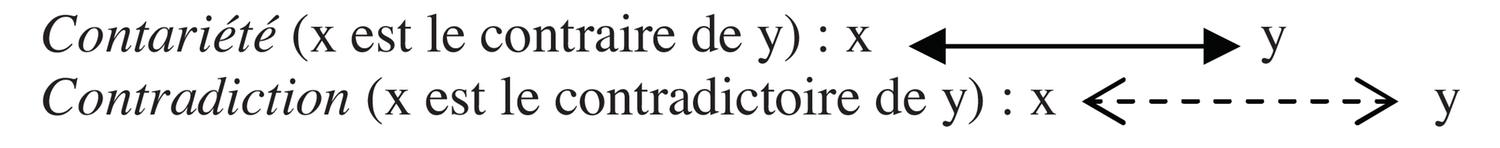
- Aristotelian family
- Classical Sigma-2
- Boolean complexity
- 3
- Number of labels per vertex (at most)
- 1
- Uniqueness of the vertices up to logical equivalence
- Yes
- Errors in the diagram
- No
- Shape
- Rectangle (irregular)
- Colinearity range
- 0
- Coplanarity range
- 0
- Cospatiality range
- 0
- Representation of contradiction
- By central symmetry
Logic
Geometry
- Conceptual info
- Yes
- Mnemonic support (AEIO, purpurea ...)
- No
- Form
- none
- Label type
- symbolic
- Symbolic field
- mathematics
- Contains partial formulas or symbols
- No
- Mathematical branch
- set theory
- Contains definitions of relations
- No
- Form
- solid lines ,
- none ,
- dashed lines
- Has arrowheads
- Yes
- Overlap
- No
- Curved
- No
- Hooked
- No
- As wide as vertices
- No
- Contains text
- No
- Label type
- none
Vertex description
Edge description
- Diagram is colored
- No
- Diagram is embellished
- No
Style
Additional notes
- All intervals are defined on the real number line, with $h^\textit{min} < h^- < h^0 < h^+ < h^\textit{max}$ (cf. p. 170).
In the lower right vertex, the comma in between the two intervals should be interpreted as set-theoretical union ($\cup$).
The lower horizontal edge is visualized in the same way as the upper horizontal edge, i.e. as a contrariety. (Also cf. caption and legend.) However, the lower horizontal edge is actually a subcontrariety.