Opposition (1984), p. 84
by Englebretsen, George

Copyright according to our policy

Logic

Aristotelian family

Classical Sigma-2

Boolean complexity

3

Number of labels per vertex (at most)

2

Equivalence between (some) labels of the same vertex

No

Analogy between (some) labels of the same vertex

No

Uniqueness of the vertices up to logical equivalence

No

Errors in the diagram

No

Geometry

Shape

Three Dimensional Shape (irregular)

Colinearity range

0

Coplanarity range

0

Cospatiality range

0

Representation of contradiction

By central symmetry

Vertex description

Conceptual info

No

Mnemonic support (AEIO, purpurea ...)

Yes

Form

none

Label type

linguistic

,

symbolic

Language

English

Lexical field

syllogistics

Contains partial sentences or single words

No

Contains abbreviations

Yes

Symbolic field

logic

Contains partial formulas or symbols

Yes

Logical system

syllogistics

Edge description

Style

Diagram is colored

No

Diagram is embellished

No

Additional notes

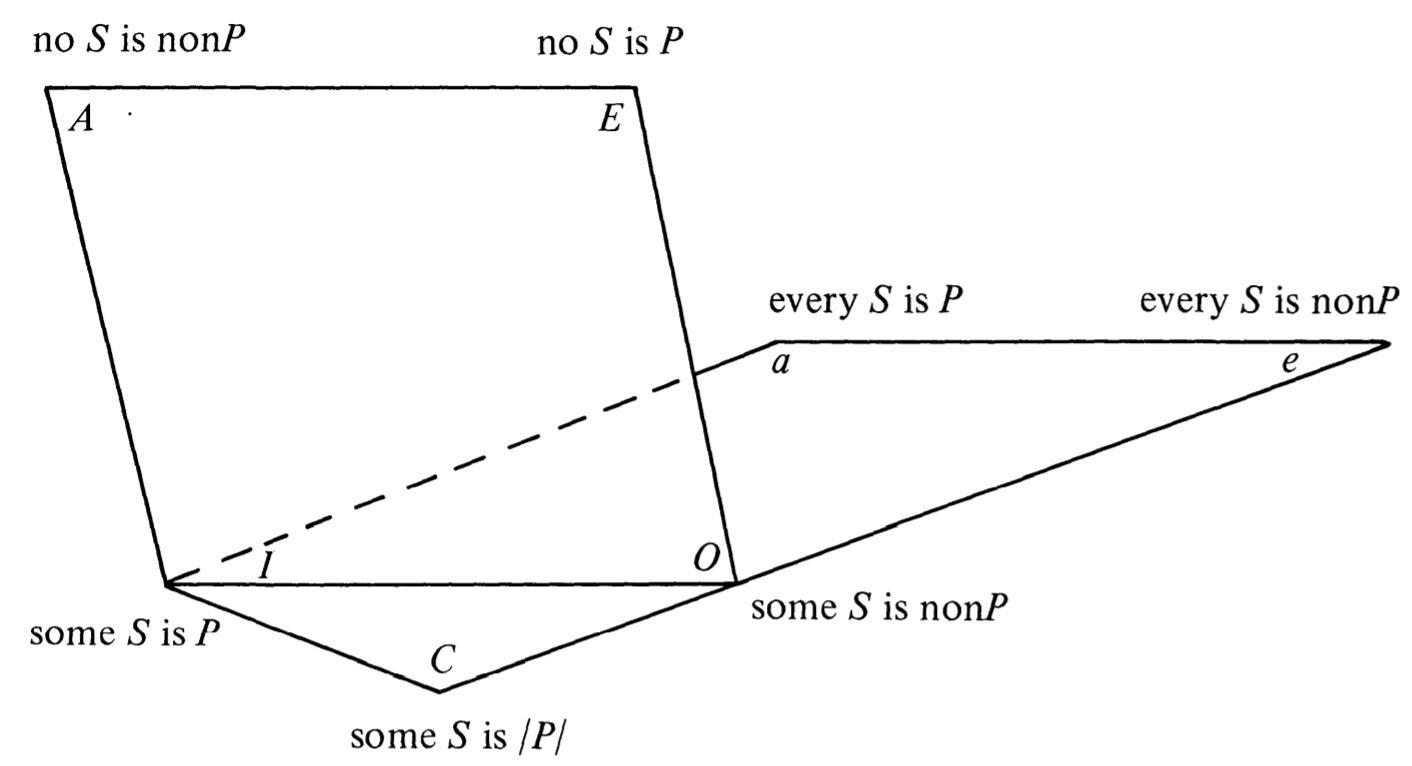
"Here AEIO is a primitive square and aeIO is a diagonal square. When I and O
are nonvacuous, both squares apply and, indeed, are identical. For nonvacuous
sentences A=a and E=e [...] For vacuous sentences only the primitive,
AEIO, square holds." (p. 83)

Given that there are subalternations from I to C and from O to C, and that I and O are subcontraries, it follows that C logically behaves like a tautology.

I entails C
O entails C
I v O is a tautology
hence C is a tautology