Structures of Opposition and Comparisons: Boolean and Gradual Cases (2020), p. 131
by Dubois, Didier; Prade, Henri; Rico, Agnès

Copyright according to our policy

Caption

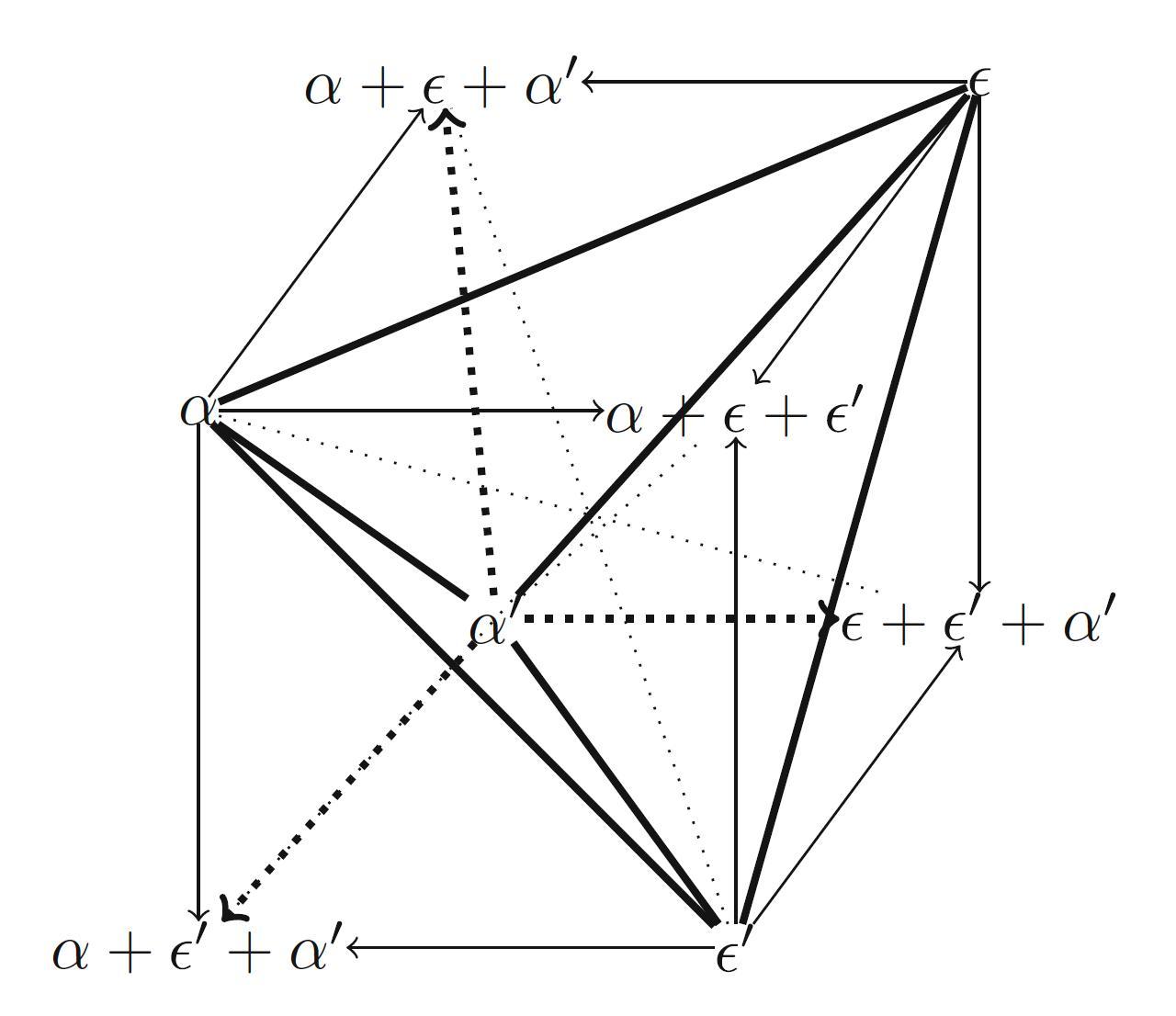
Graded version of Moretti’s cube of opposition induced by four numbers ($\alpha + \epsilon + \epsilon' + \alpha' \leq 1$)

Logic

Aristotelian family

Moretti-Pellissier Sigma-4

Boolean complexity

4–5

Number of labels per vertex (at most)

1

Uniqueness of the vertices up to logical equivalence

Yes

Errors in the diagram

No

Geometry

Shape

Cube (regular)

Colinearity range

0

Coplanarity range

0

Cospatiality range

0

Representation of contradiction

By central symmetry

Vertex description

Conceptual info

No

Mnemonic support (AEIO, purpurea ...)

No

Form

none

Label type

symbolic

Symbolic field

logic

Contains partial formulas or symbols

No

Logical system

fuzzy logic

Edge description

Style

Diagram is colored

No

Diagram is embellished

No

Additional notes

Regarding the Boolean complexity of this diagram

(i) in the caption of the figure it is stated that $\alpha + \epsilon + \epsilon' + \alpha' \leq 1$, which leaves open Boolean complexities 4 (cf. = 1) as well as 5 (cf. < 1)

(ii) later on p. 131, it is stated that $\alpha + \epsilon + \epsilon' + \alpha' = 1$, which corresponds to Boolean complexity 4