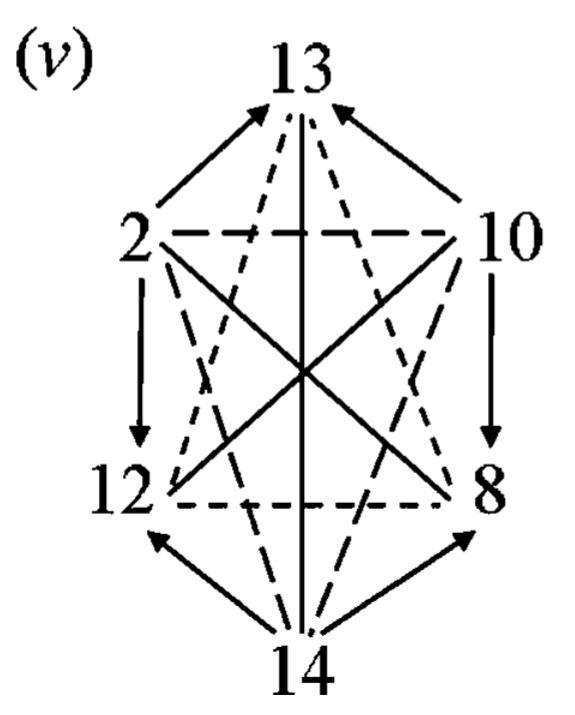
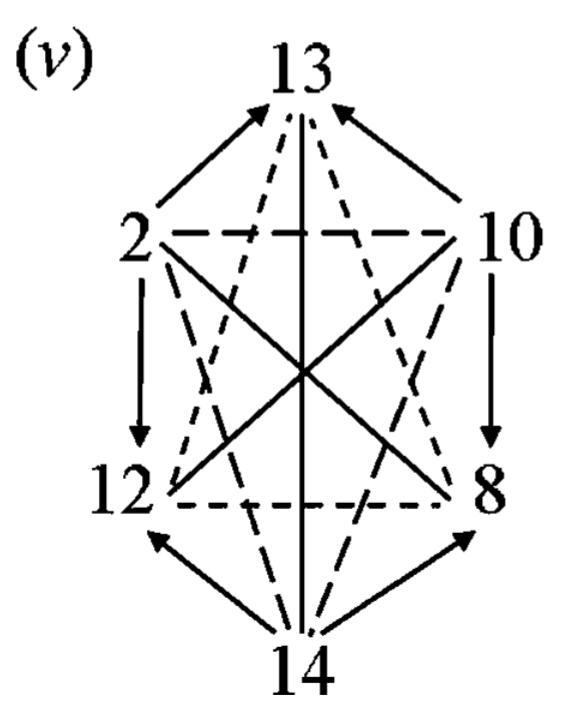
Structures of Oppositions in Public Announcement Logic (2012), p. 336
by Demey, Lorenz
Copyright according to our policy
Caption
- Six hexagons that are embeddable in the rhombic dodecahedron
- Aristotelian family
- Jacoby-Sesmat-Blanché Sigma-3
- Boolean complexity
- 3
- Number of labels per vertex (at most)
- 1
- Uniqueness of the vertices up to logical equivalence
- Yes
- Errors in the diagram
- No
- Shape
- Hexagon (irregular)
- Colinearity range
- 0
- Coplanarity range
- 0
- Cospatiality range
- 0
- Representation of contradiction
- By central symmetry
Logic
Geometry
- Conceptual info
- No
- Mnemonic support (AEIO, purpurea ...)
- No
- Form
- none
- Label type
- symbolic
- Symbolic field
- logic
- Contains partial formulas or symbols
- No
- Logical system
- epistemic logic ,
- dynamic logic
Vertex description
Edge description
- Diagram is colored
- No
- Diagram is embellished
- No
- Tags
- Boolean closed ;
- Leuven
Style
Additional notes
- The numbers 1-14 stand for the following formulas from public announcement logic (cf. p. 332):
1. $\varphi$
2. $\langle!\varphi\rangle K\psi$
3. $K[!\varphi]\psi$
4. $[!\varphi]K\psi$
5. $\neg\varphi$
6. $\langle!\varphi\rangle\neg K\psi$
7. $\neg K[!\varphi]\psi$
8. $[!\varphi]\neg K\psi$
9. $\neg\varphi \wedge K[!\varphi]\psi$
10. $\neg\varphi \wedge \neg K[!\varphi]\psi$
11. $\varphi \vee \neg K[!\varphi]\psi$
12. $\varphi \vee K[!\varphi]\psi$
13. $[!\varphi]K\psi \wedge (\varphi \vee \neg K[!\varphi]\psi)$
14. $[!\varphi]\neg K\psi \wedge (\varphi \vee K[!\varphi]\psi)$