Metalogical Decorations of Logical Diagrams (2016), p. 269
by Demey, Lorenz; Smessaert, Hans
Copyright according to our policy
Caption
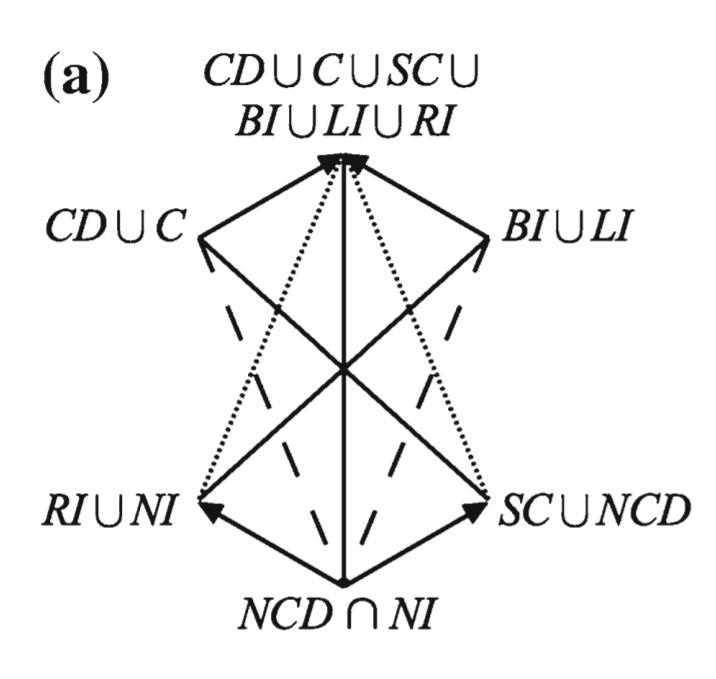
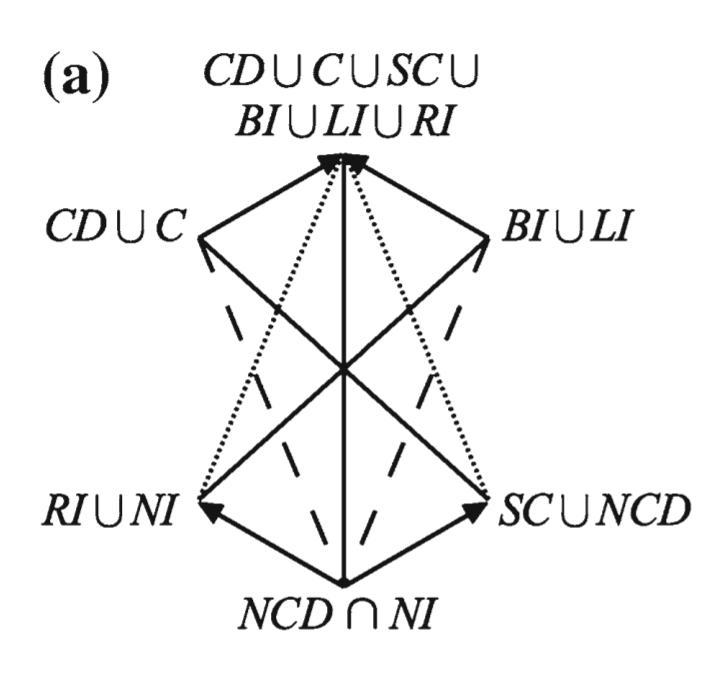
- Seuren’s relations as decorations of a an ‘unconnected-4’ hexagon (no constraints) and b a weak JSB hexagon (constraint: satisfiability of the first argument)
- Aristotelian family
- Degenerate Sigma-3 with Unconnectedness 4
- Boolean complexity
- 5
- Number of labels per vertex (at most)
- 1
- Uniqueness of the vertices up to logical equivalence
- Yes
- Errors in the diagram
- No
- Shape
- Hexagon (irregular)
- Colinearity range
- 0
- Coplanarity range
- 0
- Cospatiality range
- 0
- Representation of contradiction
- By central symmetry
Logic
Geometry
- Conceptual info
- No
- Mnemonic support (AEIO, purpurea ...)
- No
- Form
- none
- Label type
- symbolic
- Symbolic field
- metalogic
- Contains partial formulas or symbols
- No
Vertex description
Edge description
- Diagram is colored
- No
- Diagram is embellished
- No
- Tags
- Leuven
Style
Additional notes
- The 'fifth' anchor formula, which makes the difference between Boolean complexities 4 and 5, is $(\textit{RI} \cup \textit{NI}) \cap (\textit{CD} \cup \textit{C} \cup \textit{SC} \cup \textit{BI} \cup \textit{LI} \cup \textit{NI}) \cap (\textit{SC} \cup \textit{NCD})$. If $\varphi$ is a tautology and $\psi$ is contingent, then $(\varphi,\psi)$ indeed stand in the relation $(\textit{RI} \cup \textit{NI}) \cap (\textit{CD} \cup \textit{C} \cup \textit{SC} \cup \textit{BI} \cup \textit{LI} \cup \textit{NI}) \cap (\textit{SC} \cup \textit{NCD})$, so the latter is not empty, and hence, the Boolean complexity of this diagram is indeed 5 (rather than 4). Also cf. Footnote 34 on p. 268.