Metalogical Decorations of Logical Diagrams (2016), p. 267
by Demey, Lorenz; Smessaert, Hans

Copyright according to our policy

Caption

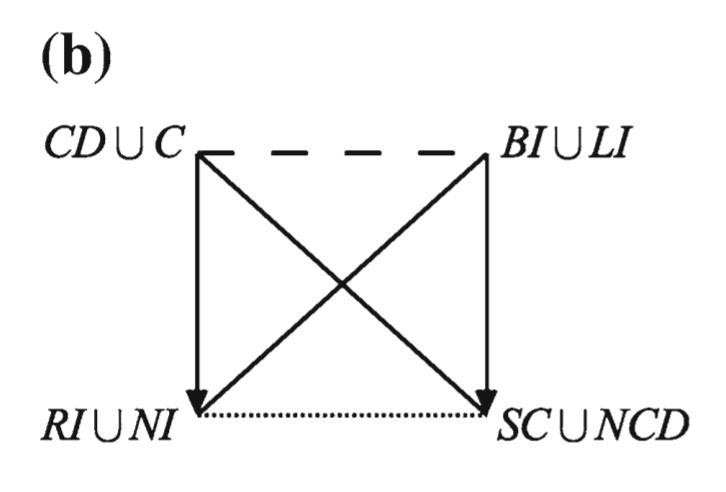
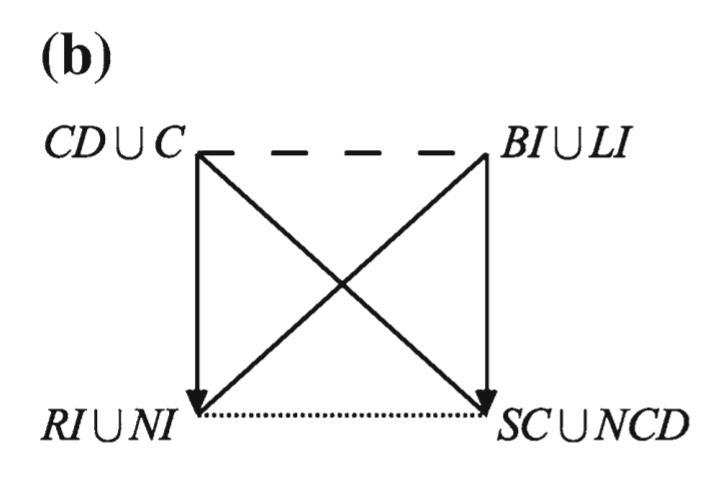
Löbner’s relations as decorations of a an Aristotelian cross (no constraints) and b a classical Aristotelian square (constraint: satisfiability of the first argument)

Logic

Aristotelian family

Classical Sigma-2

Boolean complexity

3

Number of labels per vertex (at most)

1

Uniqueness of the vertices up to logical equivalence

Yes

Errors in the diagram

No

Geometry

Shape

Rectangle (irregular)

Colinearity range

0

Coplanarity range

0

Cospatiality range

0

Representation of contradiction

By central symmetry

Vertex description

Conceptual info

No

Mnemonic support (AEIO, purpurea ...)

No

Form

none

Label type

symbolic

Symbolic field

metalogic

Contains partial formulas or symbols

No

Edge description

Style

Diagram is colored

No

Diagram is embellished

No

Tags

Leuven