Metalogical Decorations of Logical Diagrams (2016), p. 249
by Demey, Lorenz; Smessaert, Hans

Copyright according to our policy

Caption

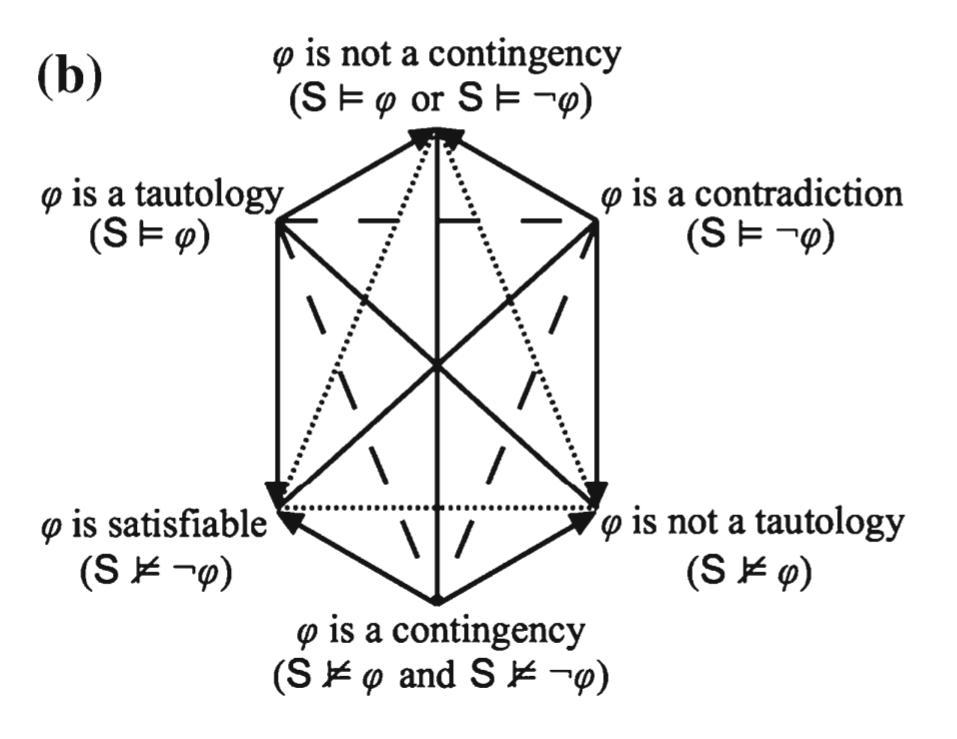
A strong Jacoby-Sesmat-Blanché hexagon for statements of the form $R(\varphi,\varphi)$ (with $R \in \wp^\cup(\mathcal{OG})$), and b its reformulation using more familiar terminology

Logic

Aristotelian family

Jacoby-Sesmat-Blanché Sigma-3

Boolean complexity

3

Number of labels per vertex (at most)

2

Equivalence between (some) labels of the same vertex

No

Analogy between (some) labels of the same vertex

No

Uniqueness of the vertices up to logical equivalence

Yes

Errors in the diagram

No

Geometry

Shape

Hexagon (irregular)

Colinearity range

0

Coplanarity range

0

Cospatiality range

0

Representation of contradiction

By central symmetry

Vertex description

Conceptual info

No

Mnemonic support (AEIO, purpurea ...)

No

Form

none

Label type

linguistic

,

symbolic

Language

English

Lexical field

metalogic

Contains partial sentences or single words

No

Contains abbreviations

No

Symbolic field

metalogic

Contains partial formulas or symbols

No

Edge description

Style

Diagram is colored

No

Diagram is embellished

No

Tags

Boolean closed

;

Leuven