Metalogical Decorations of Logical Diagrams (2016), p. 246
by Demey, Lorenz; Smessaert, Hans
Copyright according to our policy
Caption
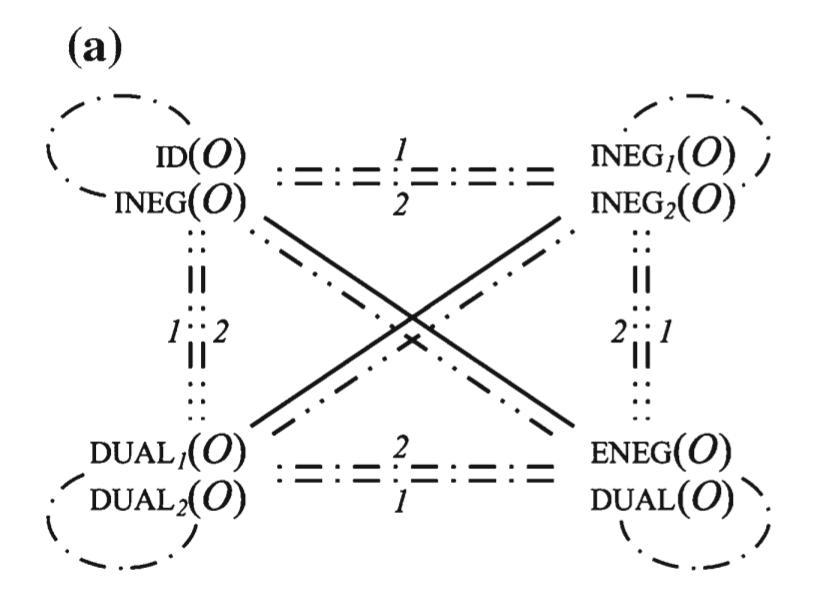
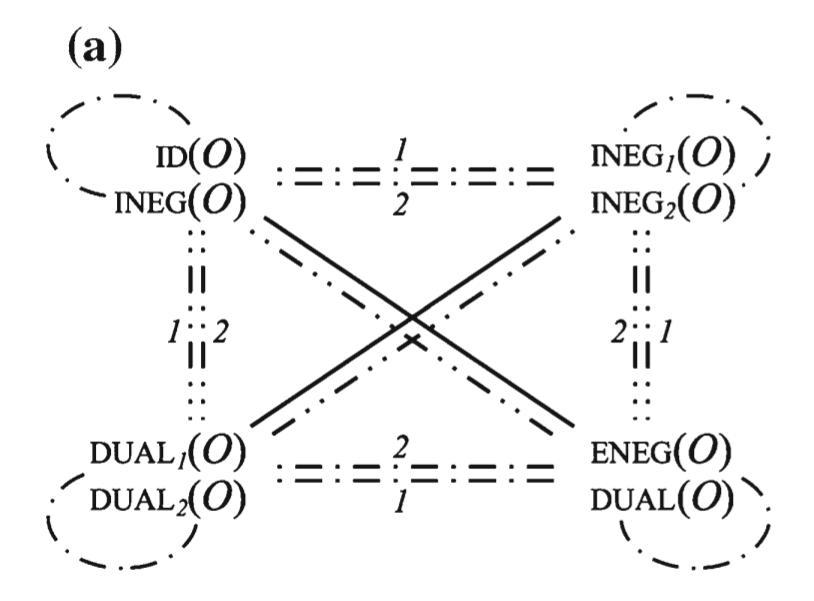
- a Degenerated generalized Post duality cube for binary operators whose $\text{INEG}_1$ and $\text{INEG}_2$ coincide, and its decomposition into two generalized Post duality squares for b $\text{INEG}_1$/$\text{DUAL}_1$ and c $\text{INEG}_2$/$\text{DUAL}_2$
- Aristotelian family
- Sigma-2 Graph
- Boolean complexity
- 3–4
- Number of labels per vertex (at most)
- 2
- Equivalence between (some) labels of the same vertex
- Yes
- Analogy between (some) labels of the same vertex
- No
- Uniqueness of the vertices up to logical equivalence
- Yes
- Errors in the diagram
- No
- Shape
- Rectangle (irregular)
- Colinearity range
- 0
- Coplanarity range
- 0
- Cospatiality range
- 0
- Representation of contradiction
- By central symmetry
Logic
Geometry
- Conceptual info
- No
- Mnemonic support (AEIO, purpurea ...)
- No
- Form
- none
- Label type
- symbolic
- Symbolic field
- logic
- Contains partial formulas or symbols
- No
- Contains definitions of relations
- No
- Form
- dash-double-dotted lines ,
- solid lines ,
- dash-dotted lines
- Has arrowheads
- No
- Overlap
- No
- Curved
- Yes
- Hooked
- No
- As wide as vertices
- No
- Contains text
- Yes
- Label type
- symbolic
- Symbolic field
- metalogic
- Contains partial formulas or symbols
- Yes
Vertex description
Edge description
- Diagram is colored
- No
- Diagram is embellished
- No
- Tags
- Leuven ;
- generalized Post duality ;
- duality
Style
Additional notes
- The edge label '1' indicates that internal negation applies to the first argument.
The edge label '2' indicates that internal negation applies to the second argument.