The Square of Opposition and Generalized Quantifiers (2012), p. 224
by D'Alfonso, Duilio

Copyright according to our policy

Caption

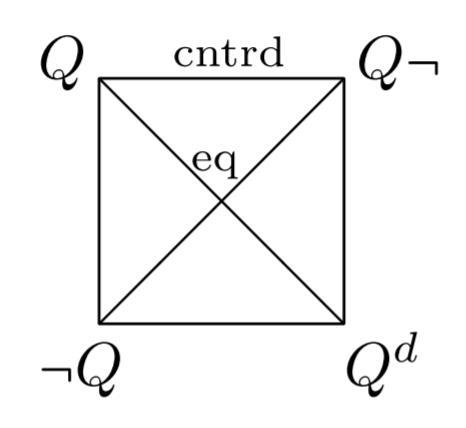
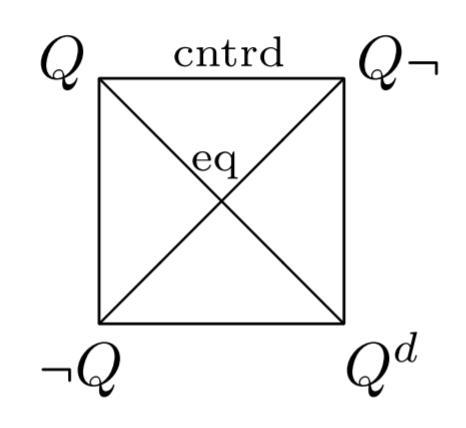
Using the modern version of the square, we can easily visualize different patterns of logical relations in the square(Q) of a quantifier Q. From left to right, the first square sketches the logical pattern for ultrafilters (Q and Q¬ are contradictory), the second for filters (Q and Q¬ are contrary), the third for intersective quantifiers (Q and Q¬ are compatible)

Logic

Aristotelian family

A Single PCD

Boolean complexity

2

Number of labels per vertex (at most)

1

Uniqueness of the vertices up to logical equivalence

No

Errors in the diagram

No

Geometry

Shape

Square (regular)

Colinearity range

0

Coplanarity range

0

Cospatiality range

0

Representation of contradiction

By some other geometric feature

Vertex description

Conceptual info

No

Mnemonic support (AEIO, purpurea ...)

No

Form

none

Label type

symbolic

Symbolic field

logic

Contains partial formulas or symbols

Yes

Logical system

generalized quantifier theory

Edge description

Style

Diagram is colored

No

Diagram is embellished

No

Tags

Boolean closed

;

duality

Additional notes

In this diagram we have $\neg Q$ logically equivalent to $Q\neg $, and $Q$ to $\neg Q\neg $.

This is a twisted square: the contradiction (external negation) relations are on the vertical edges, rather than on the diagonals.