Groups, Not Squares: Exorcizing a Fetish (2017), p. 244
by Carnielli, Walter

Copyright according to our policy
- Aristotelian family
- Classical Sigma-2
- Boolean complexity
- 3
- Number of labels per vertex (at most)
- 1
- Uniqueness of the vertices up to logical equivalence
- Yes
- Errors in the diagram
- Yes
- Shape
- Rectangle (irregular)
- Colinearity range
- 0
- Coplanarity range
- 0
- Cospatiality range
- 0
- Representation of contradiction
- By central symmetry
Logic
Geometry
- Conceptual info
- No
- Mnemonic support (AEIO, purpurea ...)
- No
- Form
- none
- Label type
- symbolic
- Symbolic field
- logic
- Contains partial formulas or symbols
- No
- Logical system
- propositional logic
- Contains definitions of relations
- No
- Form
- solid lines
- Has arrowheads
- Yes
- Overlap
- No
- Curved
- No
- Hooked
- No
- As wide as vertices
- No
- Contains text
- Yes
- Label type
- linguistic
- Language
- English
- Contains partial sentences or single words
- Yes
- Contain abbreviations
- No
Vertex description
Edge description
- Diagram is colored
- No
- Diagram is embellished
- No
Style
Additional notes
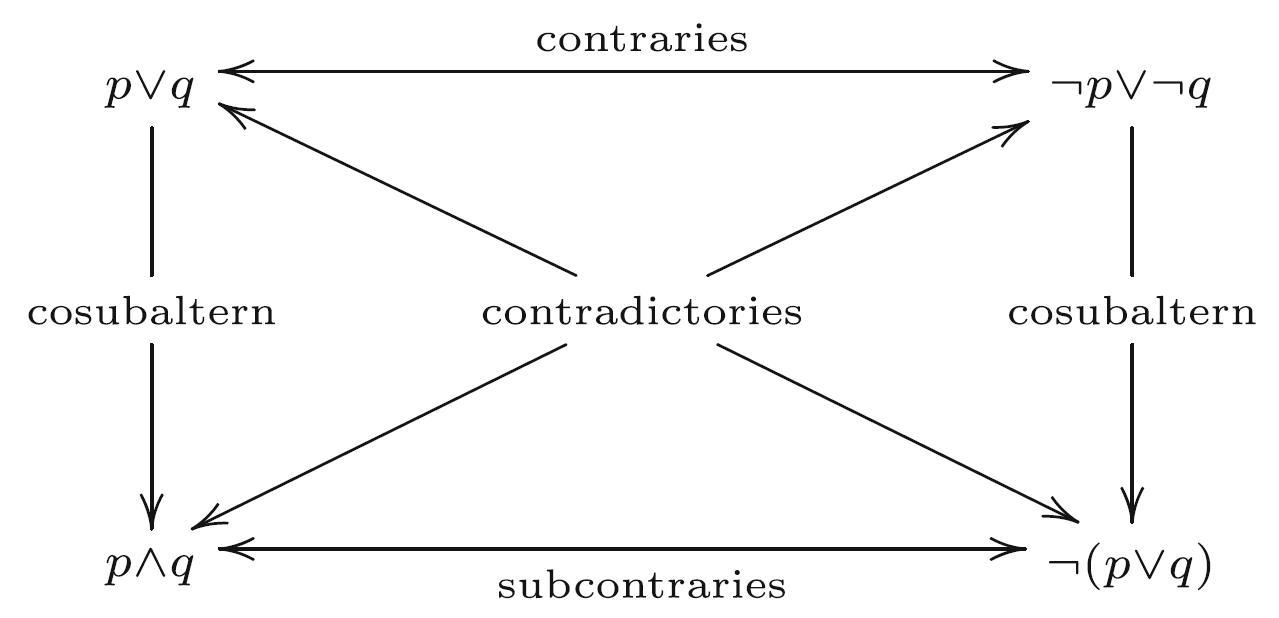
- Cosubalternation is falsity preservation (cf. p. 243); the cosubalternations shown in this diagram are indeed correct.
However:
$\bullet \ \ p \vee q$ and $\neg p \vee \neg q$ are subcontraries, rather than contraries
$\bullet \ \ p \wedge q$ and $\neg p \wedge \neg q$ are contraries, rather than subcontraries