Is There a Formula to Express the Disparatae Medieval Sentences? A Positive Answer (2017), p. 333
by Campos Benítez, Juan Manuel
Copyright according to our policy
- Aristotelian family
- Buridan Sigma-4
- Boolean complexity
- 5–6
- Number of labels per vertex (at most)
- 1
- Uniqueness of the vertices up to logical equivalence
- Yes
- Errors in the diagram
- No
- Shape
- Hexagon (irregular)
- Colinearity range
- 0
- Coplanarity range
- 2
- Cospatiality range
- 0
- Representation of contradiction
- By central symmetry
Logic
Geometry
- Conceptual info
- No
- Mnemonic support (AEIO, purpurea ...)
- Yes
- Form
- none
- Label type
- symbolic
- Symbolic field
- logic
- Contains partial formulas or symbols
- Yes
Vertex description
Edge description
- Diagram is colored
- No
- Diagram is embellished
- No
Style
Additional notes
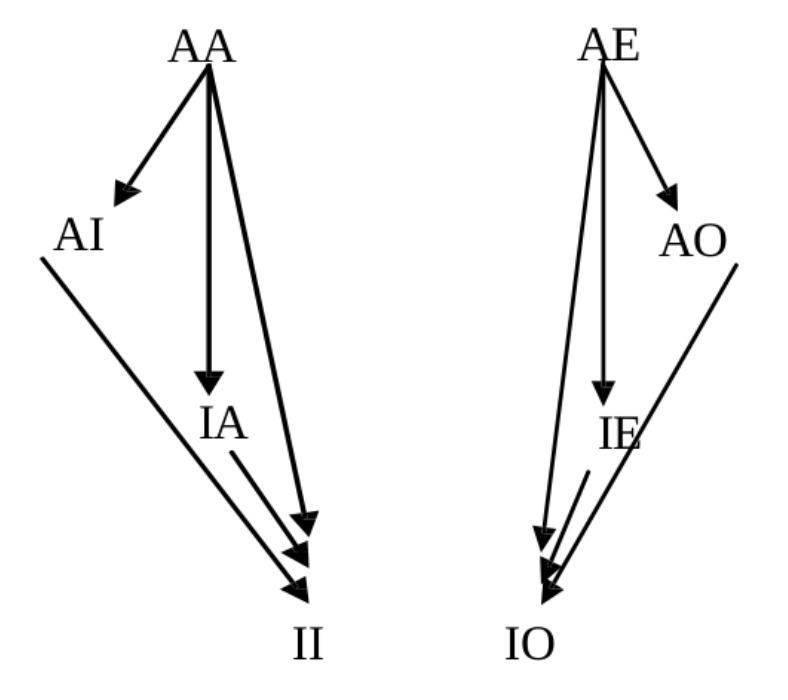
- Buridan gave three distinct octagons:
* one for modal syllogistics, in which the AA-vertex, for example, stands for 'every S is necessarily P'
* one for oblique sentences, in which the AA-vertex, for example, stands for 'every donkey of ever man runs'
* one for so-called sentences of unusual construction, in which the AA-vertex, for example, stands for 'every S every P is'
The modal oblique octagons have Boolean complexity 6, while the unusual construction octagon has Boolean complexity 5. Cf. 10.1080/01445340.2018.1531481.