The Medieval Octagon of Opposition for Sentences with Quantified Predicates (2014), p. 356
by Campos Benítez, Juan Manuel

Copyright according to our policy

Logic

Aristotelian family

A Single PCD

Boolean complexity

2

Number of labels per vertex (at most)

1

Uniqueness of the vertices up to logical equivalence

No

Errors in the diagram

No

Geometry

Shape

Rectangle (irregular)

Colinearity range

0

Coplanarity range

0

Cospatiality range

0

Representation of contradiction

By central symmetry

Vertex description

Conceptual info

No

Mnemonic support (AEIO, purpurea ...)

No

Form

none

Label type

symbolic

Symbolic field

logic

Contains partial formulas or symbols

Yes

Logical system

syllogistics

Edge description

Style

Diagram is colored

No

Diagram is embellished

No

Tags

Boolean closed

;

quantification of the predicate

Additional notes

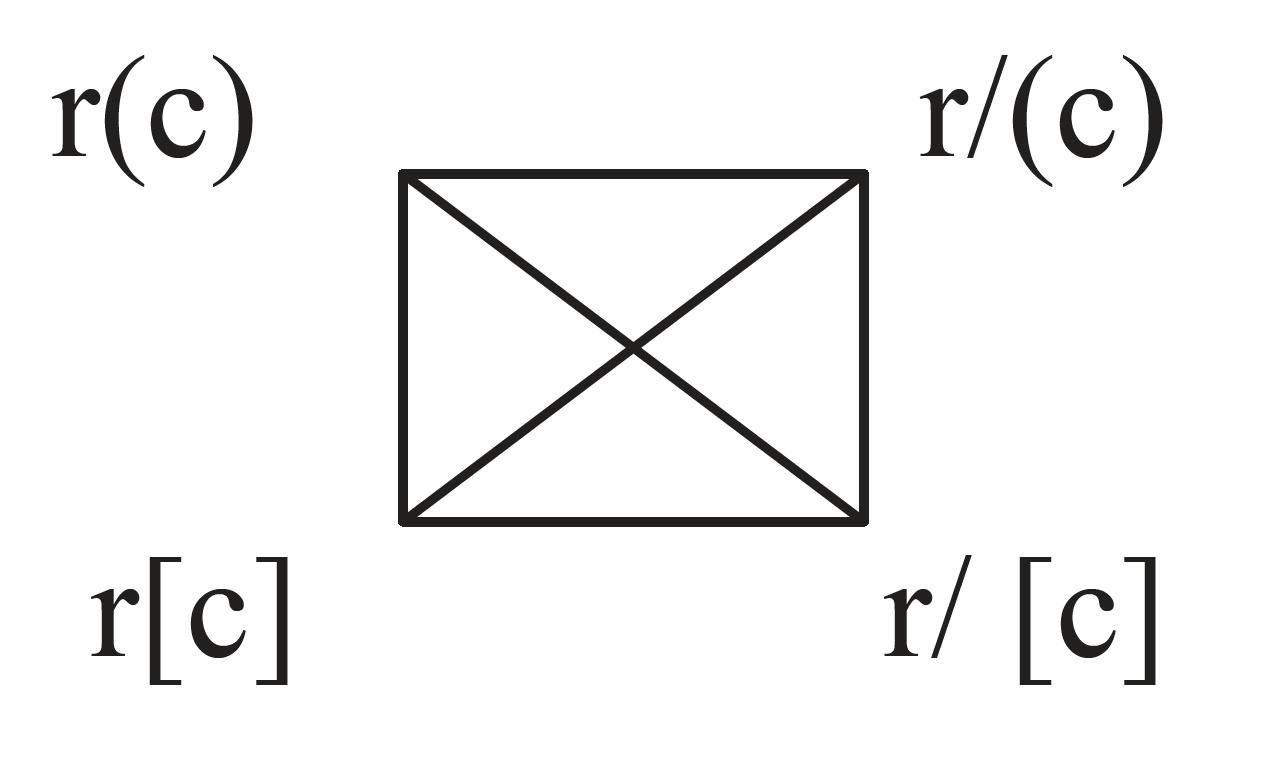
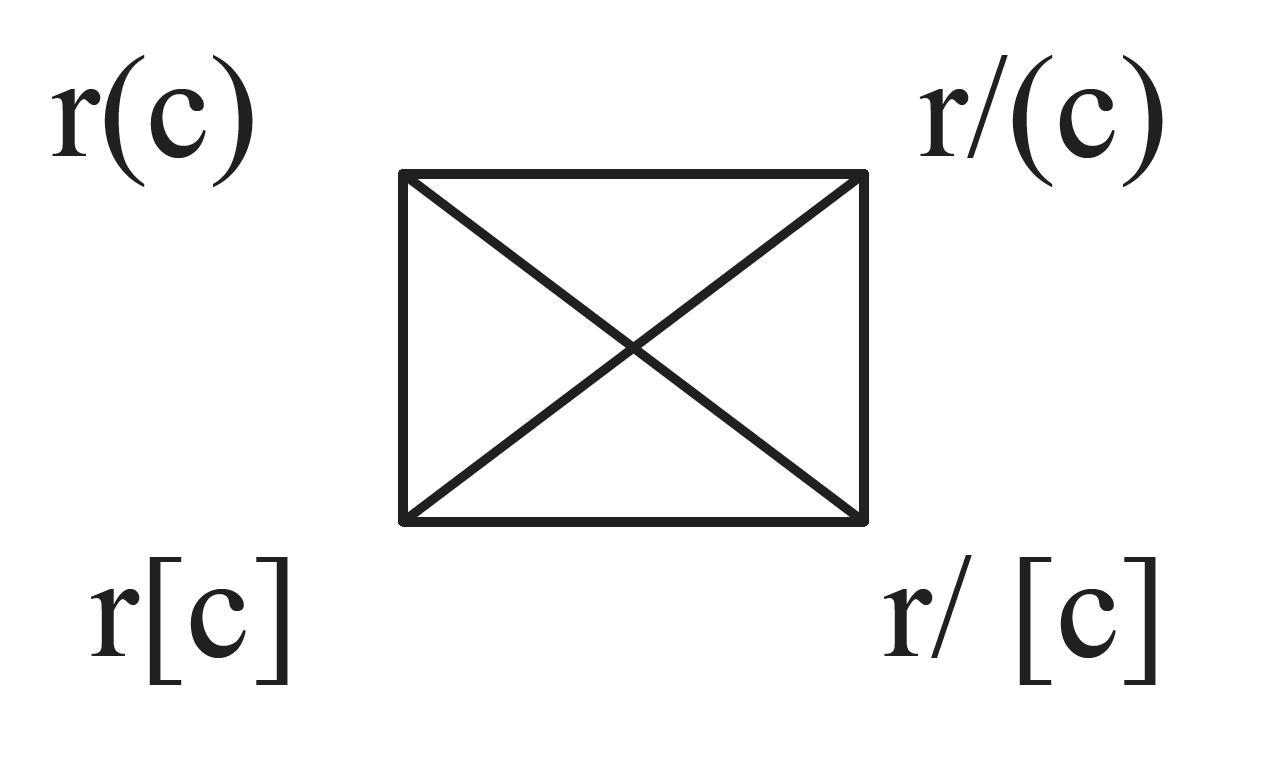
r stands for Rocinante

c stands for colt

(...) stands for universal quantification

[...] stands for existential quantification

/ stands for negation

It is assumed that there is exactly one colt in the universe, so r(c) and r[c] are logically equivalent to each other.