
Hexagon of Intelligence (2021), p. 32
by Beziau, Jean-Yves
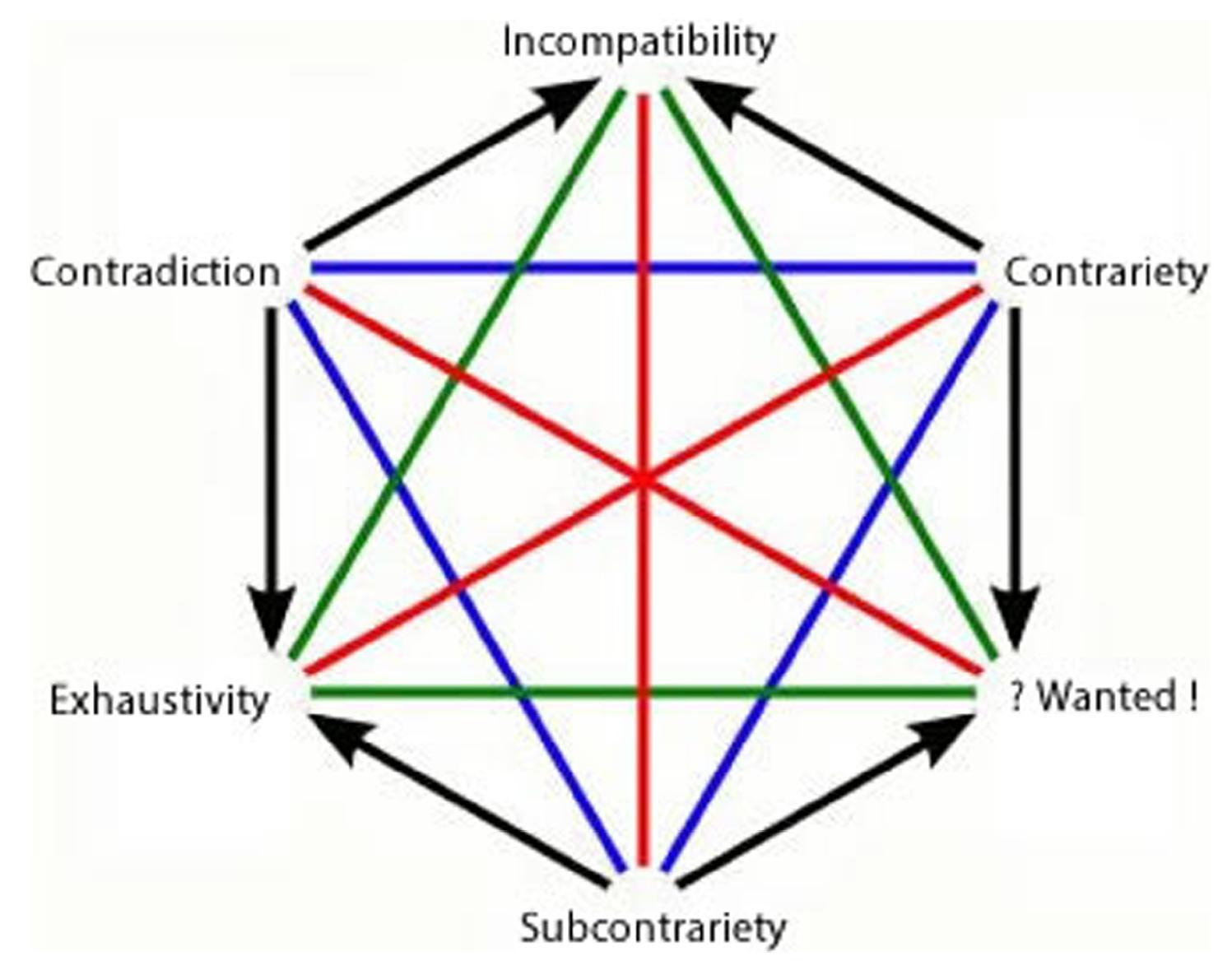
Copyright according to our policy
Caption
- The hexagon of oppositions of oppositions
- Aristotelian family
- Jacoby-Sesmat-Blanché Sigma-3
- Boolean complexity
- 3–4
- Number of labels per vertex (at most)
- 1
- Uniqueness of the vertices up to logical equivalence
- Yes
- Errors in the diagram
- Yes
- Shape
- Hexagon (regular)
- Colinearity range
- 0
- Coplanarity range
- 0
- Cospatiality range
- 0
- Representation of contradiction
- By central symmetry
Logic
Geometry
- Conceptual info
- No
- Mnemonic support (AEIO, purpurea ...)
- No
- Form
- none
- Label type
- linguistic
- Language
- English
- Lexical field
- metalogic
- Contains partial sentences or single words
- Yes
- Contains abbreviations
- No
- Contains definitions of relations
- No
- Form
- solid lines
- Has arrowheads
- Yes
- Overlap
- No
- Curved
- No
- Hooked
- No
- As wide as vertices
- No
- Contains text
- No
- Label type
- none
Vertex description
Edge description
- Diagram is colored
- Yes
- Diagram is embellished
- No
Style
Additional notes
- The most plausible interpretation of this diagram is one in which it has Boolean complexity 4 (because next to CD, C and SC, there is still a fourth possibility viz. NCD). However, on this interpretation, the uppermost vertex is CD v C v NCD (rather than CD v C), and thus is makes little sense to call this uppermost vertex 'incompatibility'. For example, we have NCD(p,p), yet we would not say that p is incompatible with itself.
Another interpretation of this diagram is one in which it has Boolean complexity 3, because we assume that NCD = $\emptyset$. In that case, the vertex labels are all ok. However, it is extremely implausible to assume that any two formulas are always contradictory, contrary or subcontrary to each other. (In normal circumstances, the vast majority of pairs of formulas will be NCD, rather than CD, C or SC.)

