The Mystery of the Fifth Logical Notion (Alice in the Wonderful Land of Logical Notions) (2020), p. 28
by Beziau, Jean-Yves
Copyright according to our policy
- Aristotelian family
- A Single PCD
- Boolean complexity
- 2
- Number of labels per vertex (at most)
- 1
- Uniqueness of the vertices up to logical equivalence
- Yes
- Errors in the diagram
- No
- Shape
- Square (regular)
- Colinearity range
- 0
- Coplanarity range
- 0
- Cospatiality range
- 0
- Representation of contradiction
- By central symmetry
Logic
Geometry
- Conceptual info
- No
- Mnemonic support (AEIO, purpurea ...)
- No
- Form
- none
- Label type
- linguistic
- Language
- English
- Lexical field
- metalogic ,
- nouns
- Contains partial sentences or single words
- Yes
- Contains abbreviations
- No
- Contains definitions of relations
- No
- Form
- solid lines ,
- none
- Has arrowheads
- No
- Overlap
- No
- Curved
- No
- Hooked
- No
- As wide as vertices
- No
- Contains text
- No
- Label type
- none
Vertex description
Edge description
- Diagram is colored
- Yes
- Diagram is embellished
- No
- Tags
- Boolean closed ;
- non-contingent formulas
Style
Additional notes
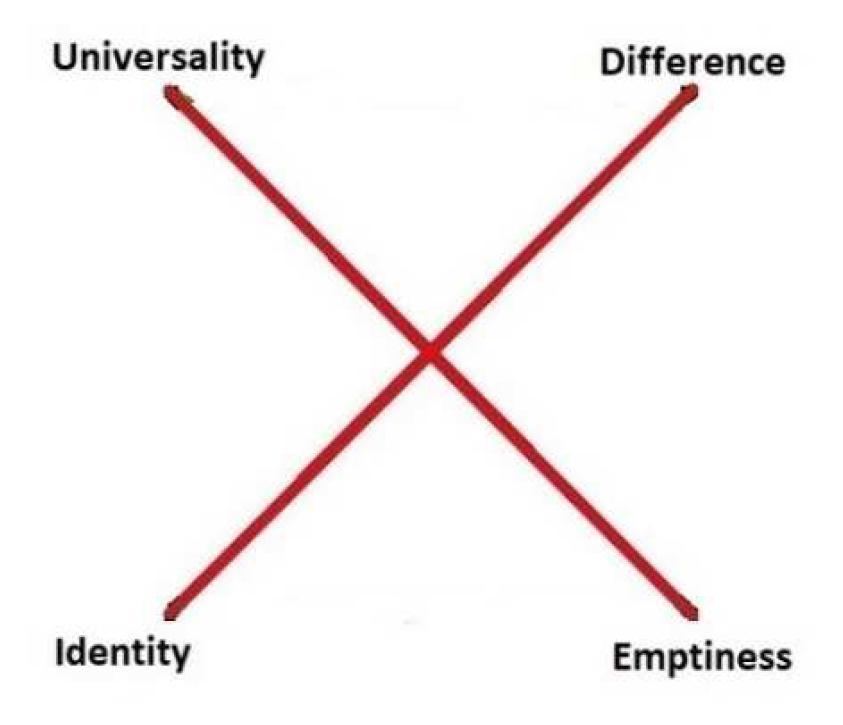
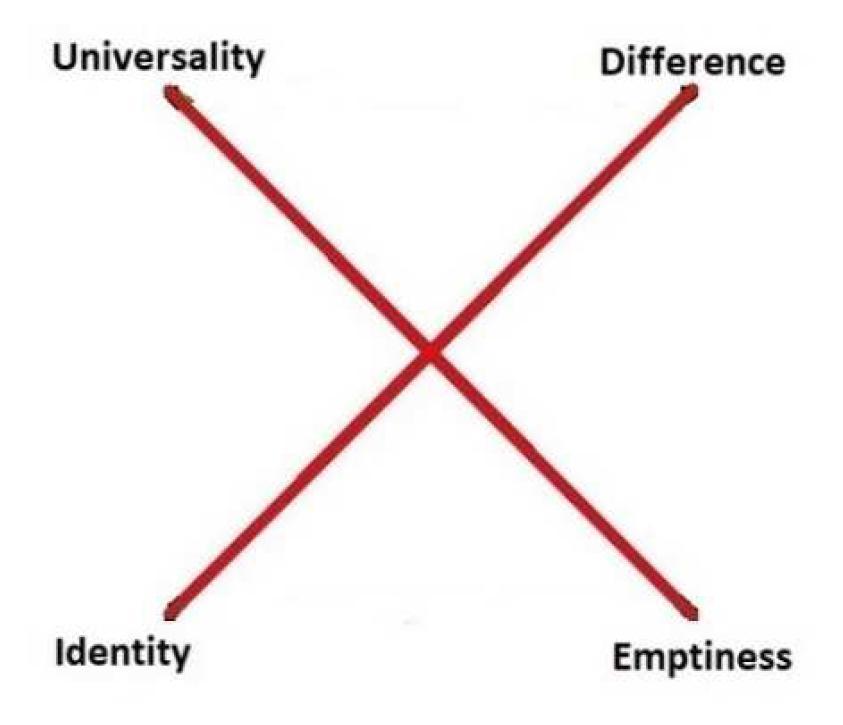
- This diagram is missing four relations; see here for the complete diagram.
Consider a domain $D$ = {a,b}, and the following relations over $D$:
* universality: {(a,a), (a,b), (b,a), (b,b)}
* emptiness: {}
* identity: {(a,a), (b,b)}
* difference: {(a,b), (b,a)}
These are binary relations over $D$, i.e. subsets of $D \times D$, or elements of $\wp(D \times D)$.
Note that universality and emptiness are resp. the top and bottom element of $\wp(D \times D)$.