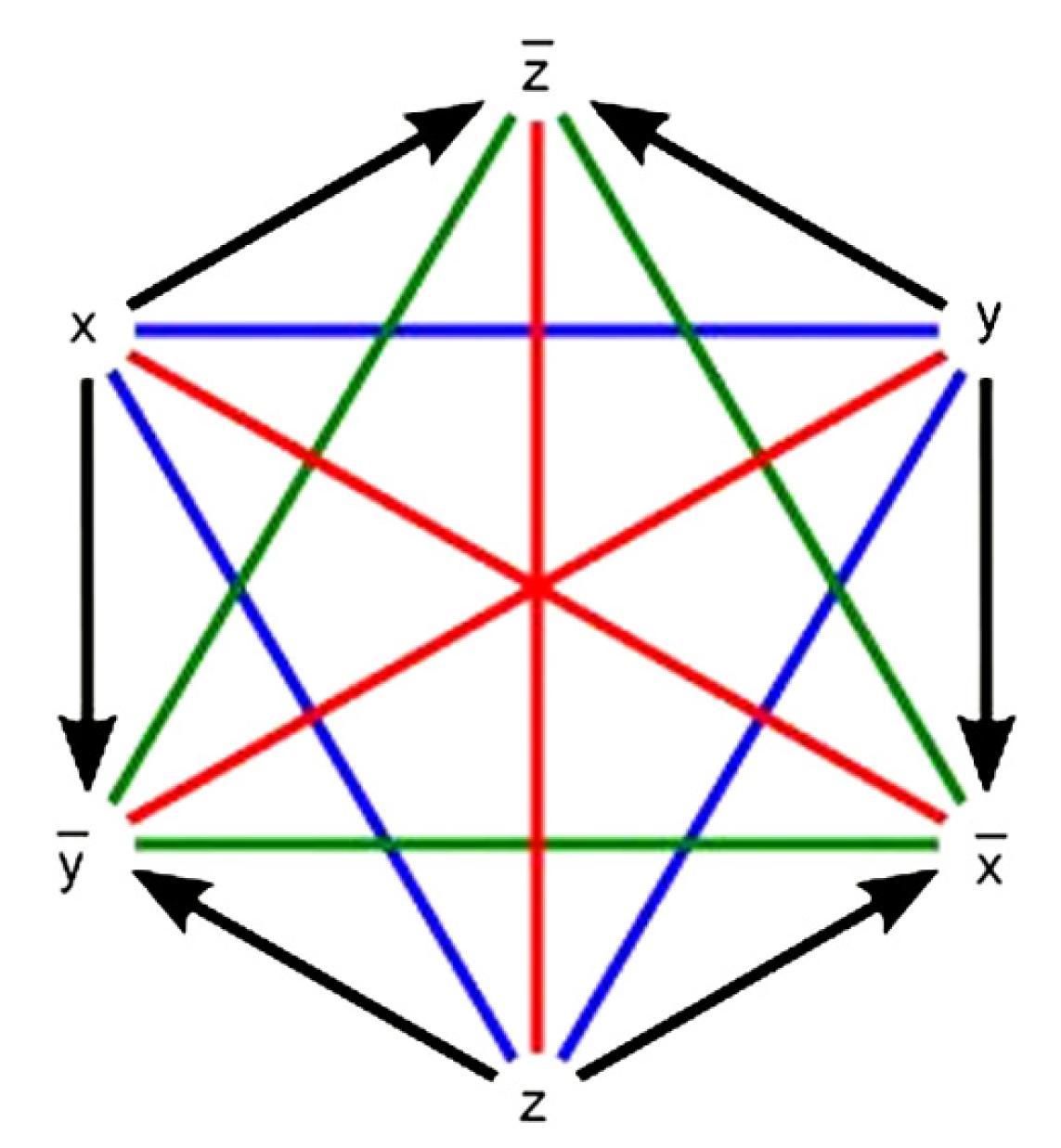
An analogical hexagon (2018), p. 8
by Beziau, Jean-Yves

Copyright according to our policy

Caption

Abstract hexagon of opposition. (For interpretation of the references to color in this figure, the reader is referred to the web version of this article.)

Logic

Aristotelian family

Jacoby-Sesmat-Blanché Sigma-3

Boolean complexity

3–4

Number of labels per vertex (at most)

1

Uniqueness of the vertices up to logical equivalence

Yes

Errors in the diagram

No

Geometry

Shape

Hexagon (regular)

Colinearity range

0

Coplanarity range

0

Cospatiality range

0

Representation of contradiction

By central symmetry

Vertex description

Conceptual info

No

Mnemonic support (AEIO, purpurea ...)

No

Form

none

Label type

generic placeholders

Edge description

Contains definitions of relations

No

Form

solid lines

Has arrowheads

Yes

Overlap

No

Curved

No

Hooked

No

As wide as vertices

No

Contains text

No

Label type

none

Style

Diagram is colored

Yes

Diagram is embellished

No

Additional notes

If the generic placeholders in this diagram satisfy the equation $z = \overline{x} \wedge \overline{y}$, then it has Boolean complexity 3 and it is Boolean closed.

If the generic placeholders do not satisfy this equation, then the diagram has Boolean complexity 4 and is not Boolean closed.