Disentangling Contradiction from Contrariety via Incompatibility (2016), p. 165
by Beziau, Jean-Yves

Copyright according to our policy

Caption

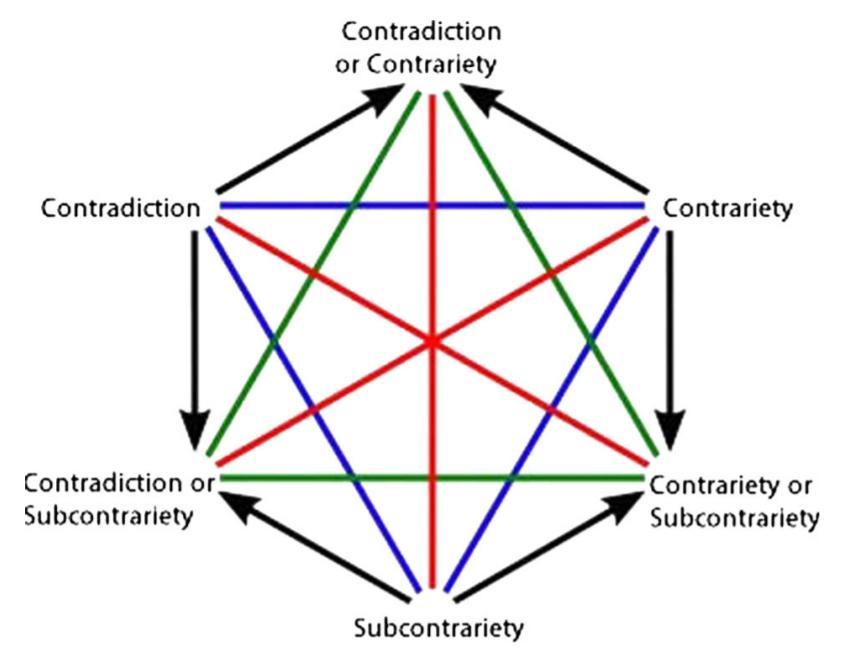
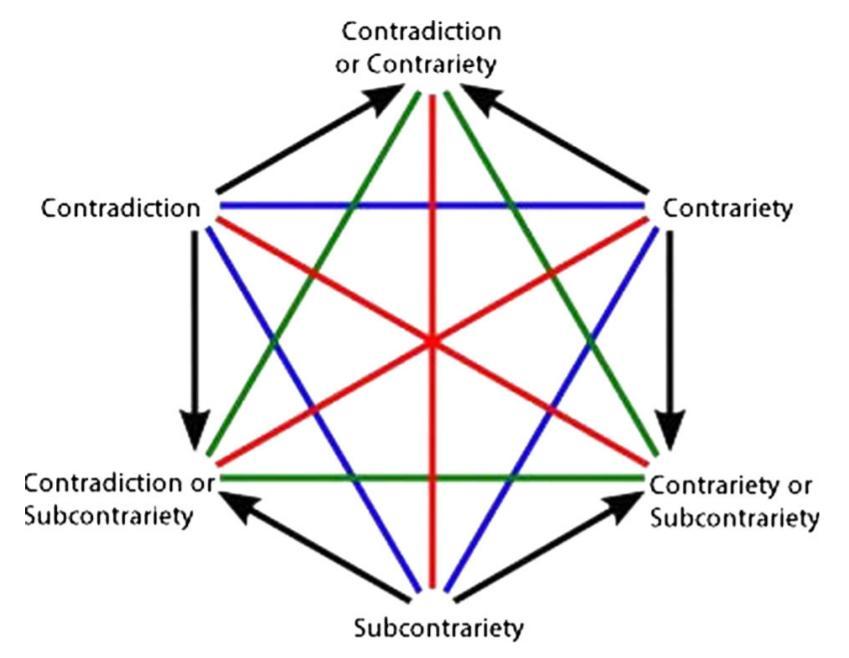
The meta-hexagon of opposition from a disjunctive perspective

Logic

Aristotelian family

Jacoby-Sesmat-Blanché Sigma-3

Boolean complexity

3–4

Number of labels per vertex (at most)

1

Uniqueness of the vertices up to logical equivalence

Yes

Errors in the diagram

Yes

Geometry

Shape

Hexagon (regular)

Colinearity range

0

Coplanarity range

0

Cospatiality range

0

Representation of contradiction

By central symmetry

Vertex description

Conceptual info

No

Mnemonic support (AEIO, purpurea ...)

No

Form

none

Label type

linguistic

Language

English

Lexical field

metalogic

Contains partial sentences or single words

Yes

Contains abbreviations

No

Edge description

Style

Diagram is colored

Yes

Diagram is embellished

No

Additional notes

The most plausible interpretation of this diagram is one in which it has Boolean complexity 4 (because next to CD, C and SC, there is still a fourth possibility viz. NCD). However, on this interpretation, the uppermost vertex is not CD v C, but rather CD v C v NCD.

Another interpretation of this diagram is one in which it has Boolean complexity 3, because we assume that NCD = $\emptyset$. In that case, the vertices are all correct. However, it is extremely implausible to assume that any two formulas are always contradictory, contrary or subcontrary to each other. (In normal circumstances, the vast majority of pairs of formulas will be NCD, rather than CD, C or SC.)