The Power of the Hexagon (2012), p. 36
by Beziau, Jean-Yves

Copyright according to our policy

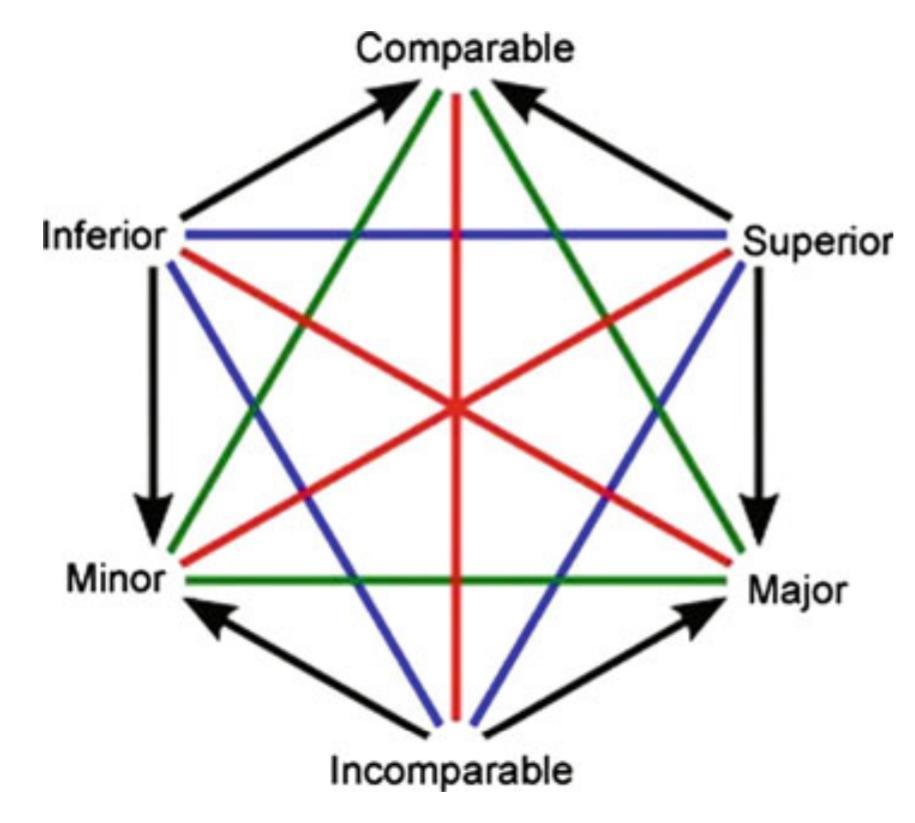
Caption

Partial order hexagon

Logic

Aristotelian family

Jacoby-Sesmat-Blanché Sigma-3

Boolean complexity

3–4

Number of labels per vertex (at most)

1

Uniqueness of the vertices up to logical equivalence

Yes

Errors in the diagram

Yes

Geometry

Shape

Hexagon (regular)

Colinearity range

0

Coplanarity range

0

Cospatiality range

0

Representation of contradiction

By central symmetry

Vertex description

Conceptual info

No

Mnemonic support (AEIO, purpurea ...)

No

Form

none

Label type

linguistic

Language

English

Lexical field

adjectives

Contains partial sentences or single words

Yes

Contains abbreviations

No

Edge description

Style

Diagram is colored

Yes

Diagram is embellished

No

Additional notes

A partial order gives rise to 4 fundamental contraries: <,>, = and incomparable. This diagram seems to identify = with incomparable.