
Two Logics of Modality (1954), p. 46
by Barber, Richard L.
Copyright according to our policy
- Aristotelian family
- Sherwood-Czeżowski Sigma-3
- Boolean complexity
- 4
- Number of labels per vertex (at most)
- 1
- Uniqueness of the vertices up to logical equivalence
- Yes
- Errors in the diagram
- No
- Shape
- Hexagon (regular)
- Colinearity range
- 0
- Coplanarity range
- 0
- Cospatiality range
- 0
- Representation of contradiction
- By central symmetry
Logic
Geometry
- Conceptual info
- No
- Mnemonic support (AEIO, purpurea ...)
- No
- Form
- none
- Label type
- symbolic
- Symbolic field
- logic
- Contains partial formulas or symbols
- No
- Logical system
- modal logic
Vertex description
Edge description
- Diagram is colored
- No
- Diagram is embellished
- No
- Tags
- Kant
Style
Additional notes
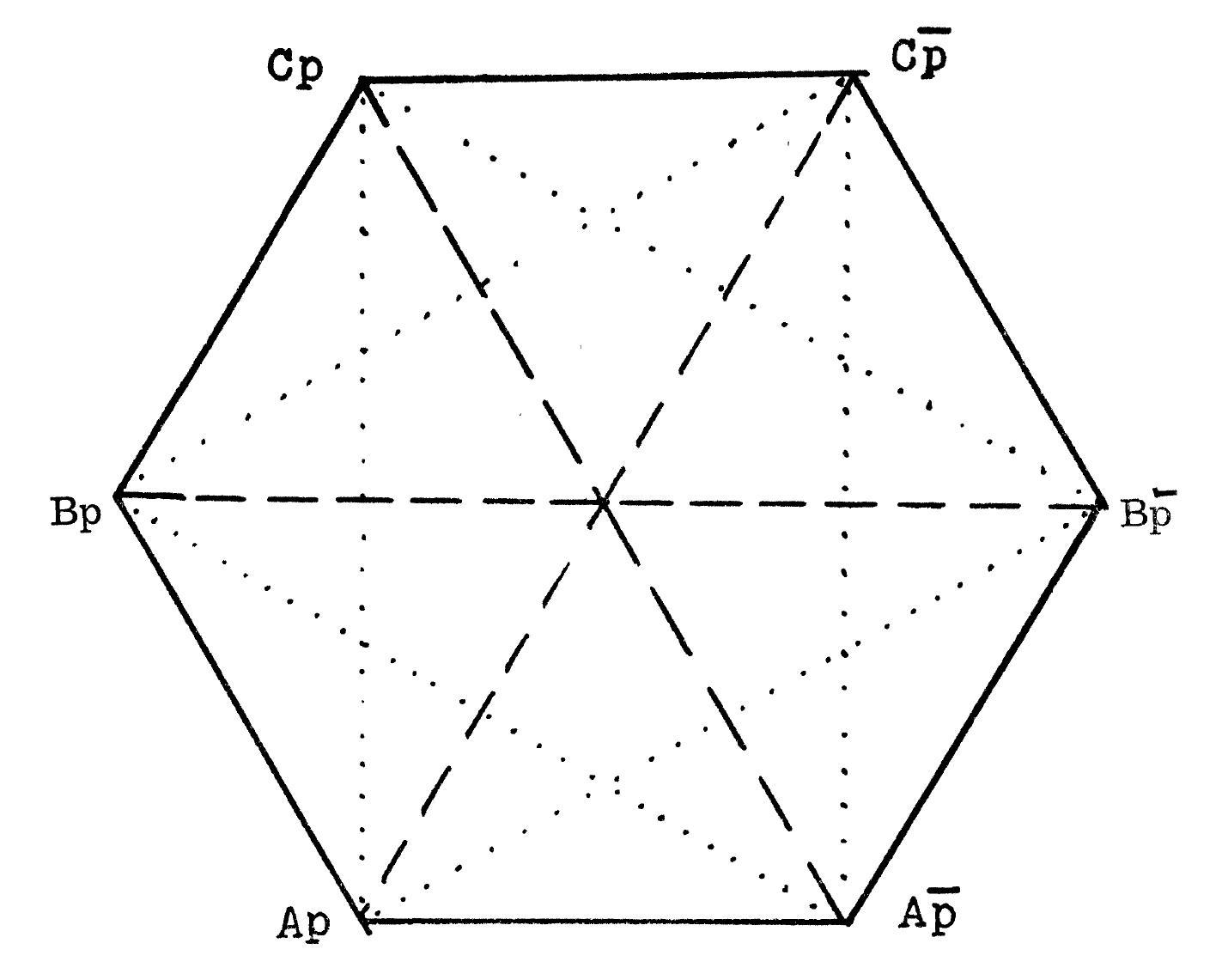
- Cf. p. 45:
$\text{Ap}$: $\text{p}$ is problematically asserted
$\text{A}\overline{\text{p}}$: $\text{p}$ is problematically negated
$\text{Bp}$: $\text{p}$ is assertorically asserted
$\text{B}\overline{\text{p}}$: $\text{p}$ is assertorically negated
$\text{Cp}$: $\text{p}$ is apodeictically asserted
$\text{C}\overline{\text{p}}$: $\text{p}$ is apodeictically negated